早教吧作业答案频道 -->数学-->
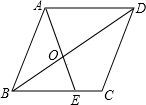
如图,已知E为菱形ABCD的边BC上一点,且AB=AE,AE交BD于点O,∠DAE=2∠BAE,证明EB=OA.
题目详情
如图,已知E为菱形ABCD的边BC上一点,且AB=AE,AE交BD于点O,∠DAE=2∠BAE,证明EB=OA.

▼优质解答
答案和解析
 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,
∴AD∥BC,∠ABD=∠DBC,
∴∠DAE=∠AEB,
∵AB=AE,
∴∠ABE=∠AEB,
∵∠DAE=2∠BAE,
∴∠AEB=2∠BAE,
设∠BAE=x,则∠ABE=∠AEB=2x,
故∠BAE+∠ABE+∠AEB=180°,
即x+2x+2x=180°,
解得:x=36°,
∴∠ABE=∠AEB=72°,∠BAE=36°,
∴∠ABD=∠CBD=36°,则∠BOE=70°,
∴AO=BO,BO=BE,
∴AO=BE.
 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,∴AD∥BC,∠ABD=∠DBC,
∴∠DAE=∠AEB,
∵AB=AE,
∴∠ABE=∠AEB,
∵∠DAE=2∠BAE,
∴∠AEB=2∠BAE,
设∠BAE=x,则∠ABE=∠AEB=2x,
故∠BAE+∠ABE+∠AEB=180°,
即x+2x+2x=180°,
解得:x=36°,
∴∠ABE=∠AEB=72°,∠BAE=36°,
∴∠ABD=∠CBD=36°,则∠BOE=70°,
∴AO=BO,BO=BE,
∴AO=BE.
看了 如图,已知E为菱形ABCD的...的网友还看了以下:
已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=FC1= 2020-05-16 …
大学复变函数自创的题目:请来看看自己想的,希望可以破解.r1*e^i(w1*x+n1)+r2*e^ 2020-05-20 …
从保证的内容看,保证可分为()A.默示保证B.承诺保证C.明示保证D.确认保证E.口头保证 2020-05-22 …
几何题,求证:D,A,E三点共线.在△ABC的BC边上任取一点P,作PD∥AC,PE∥AB,PD、 2020-06-04 …
原始凭证按其取得的来源不同可分为().原始凭证按其取得的来源不同可分为(多选).A累计凭证B一次凭 2020-06-10 …
令文法G[E]为:E→T|E+T|E-TT→F|T*F|T/FF→(E)|i证明E+T*F是它的一 2020-07-08 …
下列除哪一项外是中医独特理论体系A、整体观念B、辨证论治C、恒动观念D、预防为主E、阴阳下列除哪一 2020-07-22 …
求证e^i(4π/n)+e^i(8π/n)+...+e^i4(n-1)π/n+e^i(4nπ/n)= 2020-11-01 …
学数学的烦恼设G是一个2n阶有限交换群,其中n是一个奇数.证明:G有且只有一个2阶元素.证:依题意, 2020-11-03 …
如图,在已知三角形ABC中,BF垂直于AC,CE垂直于AB垂足分别为F,E,BF与CE交与点D,BD 2020-11-03 …