早教吧作业答案频道 -->数学-->
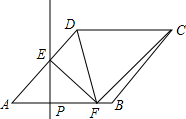
如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点,过点P作PE⊥AB交AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF为等腰三角形时,AP的长为.
题目详情
如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点,过点P作PE⊥AB交AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF为等腰三角形时,AP的长为___.

▼优质解答
答案和解析
如图1,当DF=CD时,点F与A重合或在点F′处.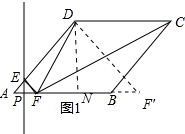
∵在菱形ABCD中,AB=4,
∴CD=AD=4,
作DN⊥AB于N,
在RT△ADN中,∵AD=4,∠DAN=45°DN=AN=NF′=2
,
∴AP=2
,
如图2,当CF=CD=4时,点F与B重合或在F′处,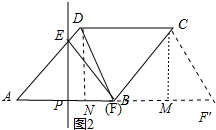
点F与B重合,PE是AB的垂直平分线,
作CM⊥AB于M,
∵CM=MF′=AN=2
,
∴AF′=4
+4,
∴AP=
AF′=2,
如图3中,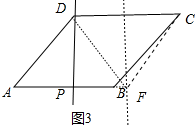 当FD=FC时,
当FD=FC时,
AF=2
+2,
∴AP=
AF=
+1.
综上所述:当△CDF为等腰三角形时,AP的长为2或
+1或2
.
故答案为:2或
+1或2
.

∵在菱形ABCD中,AB=4,
∴CD=AD=4,
作DN⊥AB于N,
在RT△ADN中,∵AD=4,∠DAN=45°DN=AN=NF′=2
| 2 |
∴AP=2
| 2 |
如图2,当CF=CD=4时,点F与B重合或在F′处,

点F与B重合,PE是AB的垂直平分线,
作CM⊥AB于M,
∵CM=MF′=AN=2
| 2 |
∴AF′=4
| 2 |
∴AP=
| 1 |
| 2 |
如图3中,
 当FD=FC时,
当FD=FC时,AF=2
| 2 |
∴AP=
| 1 |
| 2 |
| 2 |
综上所述:当△CDF为等腰三角形时,AP的长为2或
| 2 |
| 2 |
故答案为:2或
| 2 |
| 2 |
看了 如图,在菱形ABCD中,∠D...的网友还看了以下:
《伦敦协会海上运输货物保险条款》将基本险的保险责任分为( )。A. I.C.C、F.P.A.和W.A 2020-05-22 …
《伦敦协会海上运输货物保险条款》将基本险的保险责任分为( )。A.I.C.C、F.P.A.和W.A. 2020-05-22 …
概率题,设p(A)=x,p(B)=y且p(A交B)=z,求p(A的逆交B). 2020-05-23 …
非互斥事件如何相加比如说A与B的交集不为空集(A与B互为非互斥事件)那么P(A并B)=P(A)+P 2020-06-08 …
P(A)P(B)和P(AB),P(A交B)三者的关系?P(A)+P(B)和P(A并B)的关系? 2020-06-12 …
如图,点P是函数y=4/x在第一象限的图像上的任意一点,点P关于原点的对称点是P’,过点P做PA平 2020-07-29 …
P(A并B)=P(A)+P(B)-P(A交B)这个我没看懂.这是求并集为什么还要减去A和B的交集? 2020-07-30 …
P(A交B)=0.7,P(A交(B的补集))=0.9,求P(A)?RT,求P(A)啊! 2020-07-30 …
设A为非空集合,F={f|f:A→(0,1)},证明|F|=|p(A)| 2020-08-01 …
(2007•潍坊)设P是函数y=4x在第一象限的图象上任意一点,点P关于原点的对称点为P′,过P作P 2020-11-13 …