早教吧作业答案频道 -->数学-->
如图,AB⊥BC,DC⊥BC,AB=6,BC=14,CD=4,点P是边BC上的一点,连接AP,过点B作BE⊥AP,垂足为E.(1)当点P在边BC上移动时(点P不与点B重合),AE•AP的值是否发生变化?若不变,求出这个值;
题目详情
如图,AB⊥BC,DC⊥BC,AB=6,BC=14,CD=4,点P是边BC上的一点,连接AP,过点B作BE⊥AP,垂足为E.
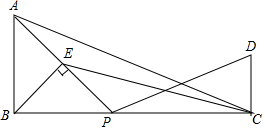
(1)当点P在边BC上移动时(点P不与点B重合),AE•AP的值是否发生变化?若不变,求出这个值;若变化,说明理由;
(2)当点P移动到BC的中点时,连接AC、BC,求证:∠PAC=∠PCE;
(3)点P在BC上移动,当以P、C、D为顶点的三角形与△PAB相似时,求PB的长.

(1)当点P在边BC上移动时(点P不与点B重合),AE•AP的值是否发生变化?若不变,求出这个值;若变化,说明理由;
(2)当点P移动到BC的中点时,连接AC、BC,求证:∠PAC=∠PCE;
(3)点P在BC上移动,当以P、C、D为顶点的三角形与△PAB相似时,求PB的长.
▼优质解答
答案和解析
(1) 结论:AE•AP的值不发生变化.AE•AP=36.
理由:∵AB⊥BC,DC⊥BC,
∴∠ABP=∠AEB,∵∠BAE=∠BAP,
∴△ABE∽△APB,
∴
=
,
∴AE•AP=AB2=36.
(2)证明:∵∠BPA=∠BPE,∠PBA=∠PEB,
∴△PBE∽△PAB,
∴
=
,∵PB=PC,
∴PC2=PE•PA,
∴
=
,∵∠CPE=∠CPA,
∴△CPE∽△APC,
∴∠PCE=∠PAC.
(3)设PB=x则PC=14-x,
①若△PBA∽△PCD,
则有
=
,
∴
=
,
∴PB=x=
.
②若若△PBA∽△DCP,
则有
=
,
∴
=
,
∴x=2或12,
∴PB=2或12,
综上所述,PB=
或2或12.
理由:∵AB⊥BC,DC⊥BC,
∴∠ABP=∠AEB,∵∠BAE=∠BAP,
∴△ABE∽△APB,
∴
| AB |
| AP |
| AE |
| AB |
∴AE•AP=AB2=36.
(2)证明:∵∠BPA=∠BPE,∠PBA=∠PEB,
∴△PBE∽△PAB,
∴
| PB |
| PA |
| PE |
| PB |

∴PC2=PE•PA,
∴
| PC |
| PE |
| PA |
| PC |
∴△CPE∽△APC,
∴∠PCE=∠PAC.
(3)设PB=x则PC=14-x,
①若△PBA∽△PCD,
则有
| PB |
| PC |
| AB |
| CD |
∴
| x |
| 14-x |
| 6 |
| 4 |
∴PB=x=
| 42 |
| 5 |
②若若△PBA∽△DCP,
则有
| PB |
| DC |
| AB |
| CP |
∴
| x |
| 4 |
| 6 |
| 14-x |
∴x=2或12,
∴PB=2或12,
综上所述,PB=
| 42 |
| 5 |
看了 如图,AB⊥BC,DC⊥BC...的网友还看了以下:
向量a垂直向量b,a模=b模=1,c模=13,c*a=3,c*b=4,求绝对值c-t1a-t2b取 2020-05-14 …
已知向量a=(cosa,sina),b=(cosb,sinb),c=(-1,0),1,求向量b-c 2020-05-15 …
一矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动,当线圈通过中性面时()A.线圈平面与磁感线方向平行 2020-06-15 …
如图,点A(3,n)在双曲线y=3x上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于 2020-07-10 …
在平面直角坐标系中,A点坐标为(1,1),B点与A点关于坐标原点对称,过动点P作x轴的垂线,垂足为 2020-07-13 …
(2013•松江区二模)已知抛物线y=-x2+bx+c经过点A(0,1),B(4,3).(1)求抛 2020-07-26 …
的图象经过A、B两点,点A、B的横坐标分别为2、4,过A作AC⊥x轴,垂足为C,且△AOC的面积等 2020-08-01 …
由于地球自转的原因,挂在绳子上的铅垂不是正好指向重力方向的,其有一定的角度偏差.请计算铅垂在a)纬度 2020-11-01 …
a,b是两个互相垂直的单位向量,且c*a=1,c*b=1,绝对值c=2^0.5,求对任意的正实数t绝 2020-12-01 …
一矩形线圈在匀强磁场中匀速转动,当线圈通过中性面时,下列说法正确的是()A.线圈平面与磁感线方向垂直 2021-01-23 …