早教吧作业答案频道 -->数学-->
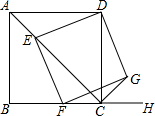
如图,已知四边形ABCD为正方形,AB=22,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②探究:CE+CG的值是否
题目详情
如图,已知四边形ABCD为正方形,AB=2
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
| 2 |
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.

▼优质解答
答案和解析
①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示: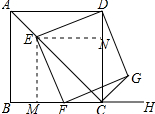
∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEM和△FEM中,
,
∴△DEM≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
② CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CE=
AB=
×2
=4,
∴CE+CG=4 是定值.

∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEM和△FEM中,
|
∴△DEM≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
② CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,
|
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CE=
| 2 |
| 2 |
| 2 |
∴CE+CG=4 是定值.
看了 如图,已知四边形ABCD为正...的网友还看了以下:
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连 2020-04-09 …
如图,矩形ABCD中,E为AD上一点,EF垂直CE交AB于F,若DE=2,矩形ABCD的周长为16 2020-04-26 …
如图,在矩形ABCD中,E是AD边上的点,且角BEC=RT角,AE=5,ED=4,则CE的长是( 2020-05-16 …
在长为12厘米的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AB、CB的长,则该矩形的面积 2020-06-18 …
在长为12cm的线段AB上任取一点C.现做一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小 2020-06-18 …
请问两个相邻矩阵是怎么回事,如何看图写出它的相邻矩阵,呢,譬如给出一个图,譬如两个三角形的一个角相 2020-07-01 …
如图,已知四边形ABCD为正方形,AB=22,点E为对角线AC上一动点,连接DE,过点E作EF⊥D 2020-07-30 …
在长为12cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小 2020-07-30 …
数学,矩形题目在矩形ABCD中,E为AD上一点,EF⊥CE交AB于点F,若DE=5,矩形的周长为16 2020-12-01 …
有关有向图用邻接矩阵存储的时间复杂度1.用邻接矩阵存储有n个顶点和e条边的有向图,在邻接矩阵中删除结 2021-01-14 …