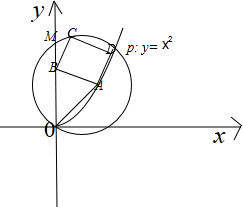
已知点A在曲线P：y=x2（x>0）上，A过原点O，且与y轴的另一个交点为M．若线段OM，A和曲线P上分别存在点B、点C和点D，使得四边形ABCD（点A，B，C，D顺时针排列）是正方形，则称点A为曲线P

Question

已知点A在曲线P：y=x²（x>0）上， A过原点O，且与y轴的另一个交点为M．若线段OM， A和曲线P上分别存在点B、点C和点D，使得四边形ABCD（点A，B，C，D顺时针排列）是正方形，则称点A为曲线P的“完美点”．那么下列结论中正确的是（　　）

A. 曲线P上不存在“完美点”

B. 曲线P上只存在一个“完美点”，其横坐标大于1

C. 曲线P上只存在一个“完美点”，其横坐标大于

(1)/(2)且小于1

D. 曲线P上存在两个“完美点”，其横坐标均大于

(1)/(2)

Answer 1

如下图左，如果点A为“完美点”，则AB=AD=(√(2))/(2)AC=(√(2))/(2)OA，
以A为圆心，(√(2))/(2)OA为半径作圆T（如下图右中虚线圆），
交y轴于点B，B′（可重合），交抛物线于点D，D′，
点A为“完美点”当且仅当AB⊥AD，若下图右，
（结合图象知，B点一定是上方的交点，否则在抛物线上不存在D点使得AB⊥AD；
D也一定是上方的交点，否则A，B，C，D不是顺时针），
，，
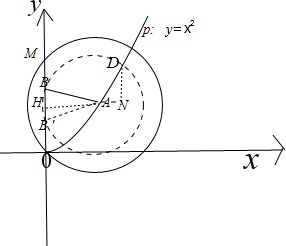下面考虑当点A的横坐标越来越大时∠BAD的变化情况，
设A（m，m²），当m<1时，∠AOY=45°，
此时圆T与y轴相离或相切时，此时A不是完美点，
故只需考虑m≥1，当m增加时，∠BAD越来越小，且趋近于0，（推理在后面），
而当m=1时，∠BAD>90°，
故曲线P上存在唯一一个完美点，其横坐标大于1，
当m增加时，∠BAD越来越小，且趋近于0°的推理：
过A作AH⊥y轴于点H，
分别过点A，D作x轴，y轴的平行线交于N，
先考虑∠BAH：cos∠BAH=(m)/((√(2))/(2)√(m2+m4))=(√(2))/(√(1+m2))，
于是m增大时，cos∠BAH减小且趋于0，从而∠BAH增大，且趋于90°，
再考虑∠DAN，记D（n，n²），则tan∠DAN=(n2-m2)/(n-m)=n+m，
随着m的增大，OA的长增大，AD=

√(作业帮用户2017-05-13问题解析假设点A为“完美点”，画出图象，设A（m，m2），通过讨论m<1时，m≥1时的情况从而得到答案．名师点评本题考点：二次函数的性质考点点评：本题考查了新定义问题，考查了二次函数的性质，考查了数形结合思想，本题有一定难度．扫描下载二维码©2019 作业帮 联系方式：[e-mail]作业帮协议)