早教吧作业答案频道 -->数学-->
在△ABC中,AC=BC,∠C=90°,将一块等腰直角三角尺的直角顶点放在斜边AB的中点P处,绕点P旋转(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.(2)如
题目详情
在△ABC中,AC=BC,∠C=90°,将一块等腰直角三角尺的直角顶点放在斜边AB的中点P处,绕点P旋转
(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.
(2)如图2,三角尺的两条直角边分别交射线AC,射线BC于D,E两点.(1)中的结论还成立吗?请说明理由.
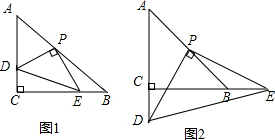
(1)如图1,三角尺的两条直角边分别交边AC,BC于D,E两点,求证:△PDE为等腰三角形.
(2)如图2,三角尺的两条直角边分别交射线AC,射线BC于D,E两点.(1)中的结论还成立吗?请说明理由.

▼优质解答
答案和解析
(1)证明:连接CP,如图1所示: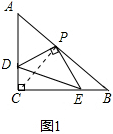
∵AC=BC,∠C=90°,P为斜边的中点,
∴PC⊥AB,PC=
AB=PB,∠PCD=∠B=45°,
∴∠BPE+∠EPC=90°,∠DPC+∠EPC=90°,
∴∠BPE=∠PCD,
在△PBE和△PCD中,
,
∴△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形;
(2)结论成立;理由如下:
连接CP,如图所示: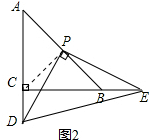
由(1)得:∠BPE=∠PCD,∠PCD=90°+45°=135°,∠PBE=180°-45°=135°,
∴∠PCD=∠PBE,
同(1)可证:△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形.

∵AC=BC,∠C=90°,P为斜边的中点,
∴PC⊥AB,PC=
| 1 |
| 2 |
∴∠BPE+∠EPC=90°,∠DPC+∠EPC=90°,
∴∠BPE=∠PCD,
在△PBE和△PCD中,
|
∴△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形;
(2)结论成立;理由如下:
连接CP,如图所示:

由(1)得:∠BPE=∠PCD,∠PCD=90°+45°=135°,∠PBE=180°-45°=135°,
∴∠PCD=∠PBE,
同(1)可证:△PBE≌△PCD(ASA),
∴PE=PD,
即△PDE为等腰三角形.
看了 在△ABC中,AC=BC,∠...的网友还看了以下:
4.如图等腰梯形ABCD中,AD=2,BC=4,腰DC=2,求高DF的长和梯形的面积. 2020-05-16 …
如图(1)是由三个等边三角形组成的图案,图中有1个等腰梯形,则第n个图中有个等腰梯如图(1)是由三 2020-06-27 …
如图是一个四面体的三视图,这个三视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的 2020-06-30 …
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则 2020-06-30 …
将“等腰三角形三线合一”的性质用符号表示今明两天就要快点!(1)等腰三角形底边上的高平分底边和顶角 2020-07-01 …
一空间几何体的三视图如图所示,其中正视图与俯视图均为边长为2的正方形,侧视图为腰长为2的等腰直角三 2020-07-13 …
怎样求等腰梯形的腰长等腰梯形ABCD中,AD=2,BC=4,高DF=2,求腰DC的长.最好再有些算 2020-08-02 …
如图,在等腰三角形ABC中,AB=AC,点D、E分别为两腰中点,BE与CD交于点F.(1)写出图中 2020-08-03 …
如图,在三角形abc中,ab=2√2,bc=6,∠abc=45°,ad∥bc,点p是射线ad上的一个 2020-11-03 …
在△ABC中,AB=2√2,BC=6,∠ABC=45°,AD‖BC,点P在射线AD上一个动点(与点A 2020-11-04 …