早教吧作业答案频道 -->数学-->
如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:(1)∠OAE=∠OBE;(2)AE=BE+2OE.
题目详情
如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:
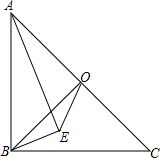
(1)∠OAE=∠OBE;
(2)AE=BE+
OE.

(1)∠OAE=∠OBE;
(2)AE=BE+
| 2 |
▼优质解答
答案和解析
证明:(1)在等腰Rt△ABC中,O为斜边AC的中点,
∴OB⊥AC,
∴∠AOB=90°,
∵∠AEB=90°,
∴A,B,E,O四点共圆,
∴∠OAE=∠OBE;
(2)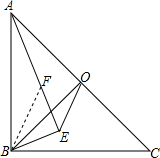 在AE上截取EF=BE,则△EFB是等腰直角三角形,
在AE上截取EF=BE,则△EFB是等腰直角三角形,
∴
=
,∠FBE=45°,
∵在等腰Rt△ABC中,O为斜边AC的中点,
∴∠ABO=45°,
∴∠ABF=∠OBE,
∵
=
,
∴
=
,
∴△ABF∽△BOE,
∴
=
,
∴AF=
OE,
∵AE=AF+EF,
∴AE=BE+
OE.
∴OB⊥AC,
∴∠AOB=90°,
∵∠AEB=90°,
∴A,B,E,O四点共圆,
∴∠OAE=∠OBE;
(2)
 在AE上截取EF=BE,则△EFB是等腰直角三角形,
在AE上截取EF=BE,则△EFB是等腰直角三角形,∴
| BF |
| BE |
| 2 |
∵在等腰Rt△ABC中,O为斜边AC的中点,
∴∠ABO=45°,
∴∠ABF=∠OBE,
∵
| AB |
| BO |
| 2 |
∴
| AB |
| BO |
| BF |
| BE |
∴△ABF∽△BOE,
∴
| AF |
| OE |
| 2 |
∴AF=
| 2 |
∵AE=AF+EF,
∴AE=BE+
| 2 |
看了 如图,在等腰Rt△ABC中,...的网友还看了以下:
已知:在平面直角坐标系xoy中,点A(0,4),点B和点C在x轴上(点B在点C的左边),点C在原点 2020-04-09 …
几ˋˊ何数学题自己先把图画出来吧图:一个由点A.B.C组成的等边三角形中,点D是边AB的中点,点E 2020-05-13 …
那咸宁中考数学的23题呢,就今年2013年的啦,阅读理解: 如图1,在四边形ABCD的边AB上任取 2020-05-16 …
如图,抛物线y=12x2-x-32与x轴交于A、B两点,D为y轴上一点,E为抛物线上一点,是否存在 2020-06-14 …
如图,抛物线y=12x2-x-32与x轴交于A、B两点,D为y轴上一点,E为抛物线上一点,是否存在 2020-06-14 …
设点C满足方程Y=2/X(X>0),以点C为圆心的圆与X轴交与E,A两点,与Y轴交与E,B两点.求 2020-07-26 …
如图,过y轴上一点A(0,1)作AC平行于X轴,交抛物线y=x?(x≥0)于点B,交抛物线y=1/ 2020-07-29 …
初中函数题解,看不明白,请教各位解答已知:在平面直角坐标系xoy中,点A(0,4),点B和点C在x轴 2020-12-13 …
如图1,图2,在△ABC中,∠ACB=90°,AC=BC,AB=8,点D时AB边长的中点,点E时AB 2021-01-12 …
初三几何综合在RT△ABC中,∠ACB=90°,tan∠BAC=1/2,点D在边AC上,不与A,C重 2021-02-04 …