早教吧作业答案频道 -->数学-->
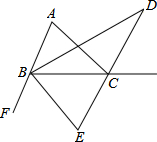
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.(1)求∠DBE的度数;(2)若∠A=70°,求∠D的度数;(3)若∠A=a,则∠D=,∠E=
题目详情
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数;
(3)若∠A=a,则∠D=___,∠E=___(用含a的式子表示)

(1)求∠DBE的度数;
(2)若∠A=70°,求∠D的度数;
(3)若∠A=a,则∠D=___,∠E=___(用含a的式子表示)
▼优质解答
答案和解析
(1)∵BD平分∠ABC,BE平分∠CBF,
∴∠DBC=
∠ABC,∠CBE=
∠CBF,
∴∠DBC+∠CBE=
(∠ABC+∠CBF)=90°,
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=
∠ACG,∠DBC=
∠ABC,
∵∠ACD=∠A+∠ABC,
∴2∠DCG=∠ACF=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=
∠A=35°;
(3)由(2)知∠D=
∠A,
∵∠A=α,
∴∠D=
α,
∵∠DBE=90°,
∴∠E=90°-
α.
故答案为:
α,90°-
α.
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DBC+∠CBE=
| 1 |
| 2 |
∴∠DBE=90°;
(2)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACD=∠A+∠ABC,
∴2∠DCG=∠ACF=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=
| 1 |
| 2 |
(3)由(2)知∠D=
| 1 |
| 2 |
∵∠A=α,
∴∠D=
| 1 |
| 2 |
∵∠DBE=90°,
∴∠E=90°-
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
看了 如图,∠CBF、∠ACG是△...的网友还看了以下:
如图所示,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向点B以2cm/s点 2020-04-11 …
设动点M与两个动点A,B所连的直线互相垂直求动点M的轨迹方程 2020-05-22 …
a、b为异面直线,夹角为60°,过空间内一点P是否有一条直线使之与a、b的夹角为20°如果a与b所 2020-06-04 …
已知直角坐标系中两点A(K,-2),B(2,T).求下列条件K,T的值,1,点A,B关于X的对称轴 2020-06-12 …
如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是整数a,b 2020-07-13 …
设AB=3cm,画图说明1.和点A,B的距离都等于2cm的所有点组成的图形;2.的点A,B的距离都 2020-07-21 …
球半径为R,A,B是球面上两点,且A,B的球面距离为(1/3)πR,则球心到过A,B所有平面的球半 2020-07-31 …
实数a∈[−1,1],b∈[0,2],设函数f(x)=−13x3+12ax2+bx的两个极值点为x1 2020-12-23 …
数轴上点A,B所代表的数为a,b,请你计算A,B两点的距离.a=2,b=6,A,B的距离是什么;a- 2020-12-30 …
如图所示为A、B两质点的v-t图象.对于A、B两质点的运动,下列说法中正确的是()A.质点A向所选定 2021-01-02 …