早教吧作业答案频道 -->数学-->
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.(1)求证:CE=EP;(2)若
题目详情
如图,边长为5的正方形OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
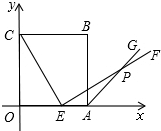
(1)求证:CE=EP;
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标:若不存在,说明理由.

(1)求证:CE=EP;
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标:若不存在,说明理由.
▼优质解答
答案和解析
(1)证明:在OC上截取OK=OE.连接EK,
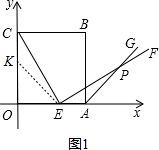
∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°,
∵AP为正方形OCBA的外角平分线,
∴∠BAP=45°,
∴∠EKC=∠PAE=135°,
∴CK=EA,
∵EC⊥EP,
∴∠CEF=∠COE=90°,
∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,
∴∠KCE=∠CEA,
在△CKE和△EAP中
∴△CKE≌△EAP,
∴EC=EP;
(2) y轴上存在点M,使得四边形BMEP是平行四边形.
如图,过点B作BM∥PE交y轴于点M,连接BP,EM,
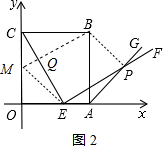
则∠CQB=∠CEP=90°,
所以∠OCE=∠CBQ,
∵在△BCM和△COE中,
∴△BCM≌△COE,
∴BM=CE,
∵CE=EP,
∴BM=EP.
∵BM∥EP,
∴四边形BMEP是平行四边形,
∵△BCM≌△COE,
∴CM=OE=3,
∴OM=CO-CM=2.
故点M的坐标为(0,2).

∵OC=OA,∠COA=∠BA0=90°,∠OEK=∠OKE=45°,
∵AP为正方形OCBA的外角平分线,
∴∠BAP=45°,
∴∠EKC=∠PAE=135°,
∴CK=EA,
∵EC⊥EP,
∴∠CEF=∠COE=90°,
∴∠CEO+∠KCE=90°,∠CEO+∠PEA=90°,
∴∠KCE=∠CEA,
在△CKE和△EAP中
|
∴△CKE≌△EAP,
∴EC=EP;
(2) y轴上存在点M,使得四边形BMEP是平行四边形.
如图,过点B作BM∥PE交y轴于点M,连接BP,EM,

则∠CQB=∠CEP=90°,
所以∠OCE=∠CBQ,
∵在△BCM和△COE中,
|
∴△BCM≌△COE,
∴BM=CE,
∵CE=EP,
∴BM=EP.
∵BM∥EP,
∴四边形BMEP是平行四边形,
∵△BCM≌△COE,
∴CM=OE=3,
∴OM=CO-CM=2.
故点M的坐标为(0,2).
看了 如图,边长为5的正方形OAB...的网友还看了以下:
求数学大神一道关于椭圆的题椭圆x/36+y/9=1上有两个动点P,Q,E(3,0),EP⊥EQ,则 2020-05-14 …
如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取 2020-05-16 …
矩形ABCD中,AB=4,BC=8将矩形ABCD绕点C顺时针旋转90°得到矩形CGEF.求点A在旋 2020-06-05 …
(2013•海南)(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E 2020-06-11 …
如图,△ABC为等边三角形,D为AC上的一点,E为AB延长线上的一点,CD=BE,DE交BC与点P 2020-06-27 …
如图,正方形ABCD,AB边上有一点E,AE=3,EB=1,在AC上有一点P,使EP+BP为最短, 2020-07-24 …
(1)如图(1),点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上 2020-07-24 …
8、△ABE中,E在圆O内,A、B在圆O上,OA、OB是定圆内任意两条半径,BE垂直AO于E,EP 2020-07-30 …
已知:如图,BP是正方形ABCD的一条外角平分线,点E在AB边上,EP⊥ED,EP交BC边于点F. 2020-08-03 …
正方形ABCD中E为BC上的任意一点,联接AE,作EF⊥AE交DCB的外角,DCH的角平分线于点P 2020-08-03 …