早教吧作业答案频道 -->数学-->
完成下面的证明(在下面的括号内填上相应的结论或推理的依据):如图,∠BED=∠B+∠D.求证:AB∥CD.证明:过点E作EF∥AB(平行公理).∵EF∥AB(已作),∴∠BEF=∠B(两直线平行,内错
题目详情
完成下面的证明(在下面的括号内填上相应的结论或推理的依据):
如图,∠BED=∠B+∠D.
求证:AB∥CD.
证明:过点E作EF∥AB(平行公理).
∵EF∥AB(已作),
∴∠BEF=∠B(两直线平行,内错角相等).
∵∠BED=∠B+∠D(已知),
又∵∠BED=∠BEF+∠FED,
∴∠FED=∠D(等量代换).
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
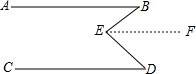
如图,∠BED=∠B+∠D.
求证:AB∥CD.
证明:过点E作EF∥AB(平行公理).
∵EF∥AB(已作),
∴∠BEF=∠B(两直线平行,内错角相等).
∵∠BED=∠B+∠D(已知),
又∵∠BED=∠BEF+∠FED,
∴∠FED=∠D(等量代换).
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).

▼优质解答
答案和解析
证明:过点E作EF∥AB.
∵EF∥AB,
∴∠BEF=∠B( 两直线平行,内错角相等).
∵∠BED=∠B+∠D,
又∵∠BED=∠BEF+∠FED,
∴∠FED=∠D.
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
故答案为:两直线平行,内错角相等,∠D,内错角相等,两直线平行,如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
∵EF∥AB,
∴∠BEF=∠B( 两直线平行,内错角相等).
∵∠BED=∠B+∠D,
又∵∠BED=∠BEF+∠FED,
∴∠FED=∠D.
∴EF∥CD(内错角相等,两直线平行).
∴AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
故答案为:两直线平行,内错角相等,∠D,内错角相等,两直线平行,如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
看了 完成下面的证明(在下面的括号...的网友还看了以下:
两道道初二数学题,在线等AB=AC,AE垂直BC1.证明AD的平方-AB的平方=BD*CD2.若D 2020-05-14 …
如图①,四边形ABCD是平行四边形,对角线AC,BD相交于点O,过点O做直线EF分别交AD,BC于 2020-05-15 …
如图1,正方形ABCD与正方形CEFG中,延长BG交DE于H.(1)求证:BH⊥DE.如图1,正方 2020-05-16 …
如图,正方形ABCD与AEFG .连接FC,取FC中点H,连接BG,BH BG与BH的数量关系是什 2020-05-16 …
已知:在四边形ABCD中,AD‖BC,∠BAC=∠D,点E、F分别在BC、CD上,且∠AEF=∠A 2020-05-17 …
高中议论文如何从“社会发展”的角度论证我主要采用递进式的论证结构,”社会发展“一般是文章第三个分论 2020-06-13 …
求分析此篇议论文结构,如:开头运用了什么什么的方法,然后哪里事例论证,道理论证,结构什么...有位 2020-06-28 …
信用证单选题下列说法错误的是()。A.信用证既可转账结算,又可支取现金B.我国信用证结算是不可撤销 2020-07-23 …
我国某公司出口布匹以信用证结算,买方银行来证规定,数量大约为5000码,每码1美元,信用证总额为5 2020-07-23 …
鄙人有个方法能证出角不能用尺规作图三等分的,初发表结论,如有不对的地方请大家多多指教,谢证法如下:已 2020-11-15 …