早教吧作业答案频道 -->数学-->
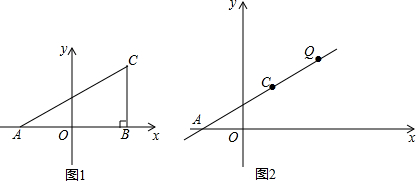
如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+b-2=0,过C作CB⊥x轴于B.(1)求三角形ABC的面积:(2)在y轴上是否存在点P,使得三角形ABC的面积和三角形ACP的面积相等
题目详情
如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积:
(2)在y轴上是否存在点P,使得三角形ABC的面积和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由:
(3)如图2,在直线AC上有一点Q(6,m),在x轴上有两动点M(c,0)、N(c+1,0),当四边形QCMN的周长最小时,求M、N的坐标.
| b-2 |
(1)求三角形ABC的面积:
(2)在y轴上是否存在点P,使得三角形ABC的面积和三角形ACP的面积相等?若存在,求出点P的坐标;若不存在,请说明理由:
(3)如图2,在直线AC上有一点Q(6,m),在x轴上有两动点M(c,0)、N(c+1,0),当四边形QCMN的周长最小时,求M、N的坐标.

▼优质解答
答案和解析
(1)∵(a+2)2+
=0,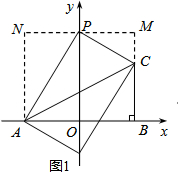
∴a+2=0,b-2=0,解得a=-2,b=2,
∴A(-2,0),C(2,2),
∴S△ABC=
AB•BC=
×4×2=4;
(2)①当P在y轴正半轴上时,如图1,
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4,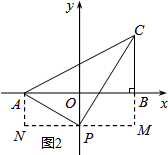
∴
-t-(t-2)=4,解得t=3,
②当P在y轴负半轴上时,如图2,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4
∴
+t-(2-t)=4,解得t=-1,
∴P(0,-1)或(0,3);
(3)如图3,作出点C关于x轴的对称点D,作DE∥x轴且DE=1,连接QE交x轴于点N,过D作DM∥QE交x轴于M,此时QE就是CM+QN的最小值,由于MN、CQ是定值,所以此时四边形QCMN周长最小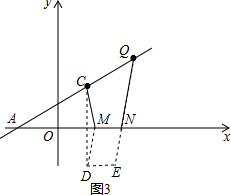 ,
,
∵A(-2,0),C(2,2),
∴直线AC的解析式为:y=
x+1,
∴Q(6,4,),
∵C(2,2),
∴D(2,-2),∴E(3,-2),
设直线QE的解析式为:y=kx+b,
∴
,
解得
,
∴直线QE的解析式为:y=2x-8,
把N(c+1,0)代入解得c=3,c+1=4,
∴M(3,0),N(4,0).
| b-2 |

∴a+2=0,b-2=0,解得a=-2,b=2,
∴A(-2,0),C(2,2),
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)①当P在y轴正半轴上时,如图1,
设P(0,t),
过P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4,

∴
| 4(t-2+t) |
| 2 |
②当P在y轴负半轴上时,如图2,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4
∴
| 4(-t+2-t) |
| 2 |
∴P(0,-1)或(0,3);
(3)如图3,作出点C关于x轴的对称点D,作DE∥x轴且DE=1,连接QE交x轴于点N,过D作DM∥QE交x轴于M,此时QE就是CM+QN的最小值,由于MN、CQ是定值,所以此时四边形QCMN周长最小
 ,
,∵A(-2,0),C(2,2),
∴直线AC的解析式为:y=
| 1 |
| 2 |
∴Q(6,4,),
∵C(2,2),
∴D(2,-2),∴E(3,-2),
设直线QE的解析式为:y=kx+b,
∴
|
解得
|
∴直线QE的解析式为:y=2x-8,
把N(c+1,0)代入解得c=3,c+1=4,
∴M(3,0),N(4,0).
看了 如图1,在平面直角坐标系中,...的网友还看了以下:
问题情境:如图1,已知△ABC和△DCE中,∠ACB=∠DCE=90°,AC=BC=2,CD=CE 2020-04-06 …
【急】在平面直角坐标系中,△ABC的两个顶点A与B在x轴上运动,且AB=2,顶点C的坐标C(0,根 2020-05-15 …
如图,一条公路修到湖边,需拐弯绕道而行,如果第一次拐的角(即∠A)是120°,第二次拐的角(即∠B 2020-05-16 …
关于勾股定理我不知道该怎么样判断勾股定理里三角形的三边关系,比如一道题,不给你给图形,让你自己画, 2020-06-10 …
线线线面交的角度范围RT.比如说二面角是[0,π]线的夹角是(0,π/2]之类的~还有蛮多的跟角有 2020-07-31 …
线线线面交的角度范围RT.比如说二面角是[0,π]线的夹角是(0,π/2]之类的~还有蛮多的跟角有 2020-07-31 …
三角形中角ABC应该是边abc谁与谁的夹角在余弦定理中cosA=(c^2+b^2-a^2)/2bc 2020-08-02 …
如图,三角形ABC是直角三角形,阴影部分1的面积比阴影部分2的面积小28平方厘米.AB长40厘米,B 2020-11-26 …
一年中,北极点的正午太阳高度角最大值为()A.66°34′B.23°26′C.0°D.90°怎么不是 2021-01-23 …
仰角是什么在三角形ABC中,CB是旗杆,小明在A点用测角仪测得旗杆顶端C的仰角为69度.仰角是∠C的 2021-02-01 …