如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠DAB=60°．侧面PAD为正三角形，且平面PAD⊥平面ABCD，则下列说法错误的是（）A.在棱AD上存在点M，使AD⊥平面PMBB.异面直线AD与PB所成的角为90°C

Question

如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠DAB=60°．侧面PAD为正三角形，且平面PAD⊥平面ABCD，则下列说法错误的是（　　）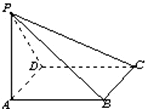

A. 在棱AD上存在点M，使AD⊥平面PMB

B. 异面直线AD与PB所成的角为90°

C. 二面角P-BC-A的大小为45°

D. BD⊥平面PAC

Answer 1

对于A，取AD的中点M，连PM，BM，则∵侧面PAD为正三角形，
∴PM⊥AD，
又底面ABCD是∠DAB=60°的菱形，
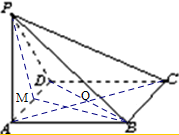
∴三角形ABD是等边三角形，
∴AD⊥BM，
∴AD⊥平面PBM，故A正确，
对于B，∵AD⊥平面PBM，
∴AD⊥PB，即异面直线AD与PB所成的角为90°，故B正确，
对于C，∵底面ABCD为菱形，∠DAB=60°平面PAD⊥平面ABCD，
∴BM⊥BC，则∠PBM是二面角P-BC-A的平面角，
设AB=1，则BM=(√(3))/(2)，PM=(√(3))/(2)，
在直角三角形PBM中，tan∠PBM=(PM)/(BM)=1，
即∠PBM=45°，故二面角P-BC-A的大小为45°，故C正确，
故错误的是D，
故选：D．