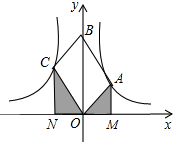
如图，OABC是平行四边形，对角线OB在轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线y=k1x和y=k2x的一支上，分别过点A、C作x轴的垂线，垂

Question

如图，OABC是平行四边形，对角线OB在轴正半轴上，位于第一象限的点A和第二象限的点C分别在双曲线y= (k1)/(x)和y= (k2)/(x)的一支上，分别过点A、C作x轴的垂线，垂足分别为M和N，则有以下的结论：
① (AM)/(CN)= (|k1|)/(|k2|)；
②阴影部分面积是 (1)/(2)（k₁+k₂）；
③当∠AOC=90°时，|k₁|=|k₂|；
④若OABC是菱形，则两双曲线既关于x轴对称，也关于y轴对称．
其中正确的结论是___（把所有正确的结论的序号都填上）．

Answer 1

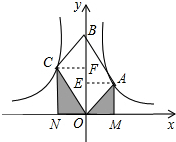作AE⊥y轴于E，CF⊥y轴于F，如图，
∵四边形OABC是平行四边形，
∴S_△AOB=S_△COB，
∴AE=CF，
∴OM=ON，
∵S_△AOM=(1)/(2)|k₁|=(1)/(2)OM•AM，S_△CON=(1)/(2)|k₂|=(1)/(2)ON•CN，
∴(AM)/(CN)=(|k1|)/(|k2|)，故①正确；
∵S_△AOM=(1)/(2)|k₁|，S_△CON=(1)/(2)|k₂|，
∴S_阴影部分=S_△AOM+S_△CON=(1)/(2)（|k₁|+|k₂|），
而k₁>0，k₂<0，
∴S_阴影部分=(1)/(2)（k₁-k₂），故②错误；
当∠AOC=90°，
∴四边形OABC是矩形，
∴不能确定OA与OC相等，
而OM=ON，
∴不能判断△AOM≌△CNO，
∴不能判断AM=CN，
∴不能确定|k₁|=|k₂|，故③错误；
若OABC是菱形，则OA=OC，
而OM=ON，
∴Rt△AOM≌Rt△CNO，
∴AM=CN，
∴|k₁|=|k₂|，
∴k₁=-k₂，
∴两双曲线既关于x轴对称，也关于y轴对称，故④正确．
故答案为：①④．