早教吧作业答案频道 -->数学-->
有两个内角分别是它们对角的一半的四边形叫做半对角四边形.(1)如图1,在半对角四边形ABCD中,∠B=12∠D,∠C=12∠A,求∠B与∠C的度数之和;(2)如图2,锐角△ABC内接于⊙O,若边AB上
题目详情
有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
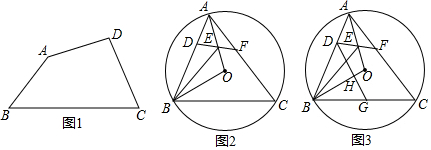
(1)如图1,在半对角四边形ABCD中,∠B=
∠D,∠C=
∠A,求∠B与∠C的度数之和;
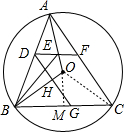
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G,当DH=BG时,求△BGH与△ABC的面积之比.

(1)如图1,在半对角四边形ABCD中,∠B=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G,当DH=BG时,求△BGH与△ABC的面积之比.
▼优质解答
答案和解析
(1)在半对角四边形ABCD中,∠B=
∠D,∠C=
∠A,
∵∠A+∠B+∠C+∠D=360°,
∴3∠B+3∠C=360°,
∴∠B+∠C=120°,
即∠B与∠C的度数和为120°;
(2)证明:∵在△BED和△BEO中
∴△BED≌△BEO,
∴∠BDE=∠BOE,
∵∠BCF=
∠BOE,
∴∠BCF=
∠BDE,
连接OC,
设∠EAF=α,则∠AFE=2∠EAF=2α,
∴∠EFC=180°-∠AFE=180°-2α,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠AOC=180°-∠OAC-∠OCA=180°-2α,
∴∠ABC=
∠AOC=
∠EFC,
∴四边形DBCF是半对角四边形;
(3) 过点O作OM⊥BC于M,
∵四边形DBCF是半对角四边形,
∴∠ABC+∠ACB=120°,
∴∠BAC=60°,
∴∠BCO=2∠BAC=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴BC=2BM=
BO=
BD,
∵DG⊥OB,
∴∠HGB=∠BAC=60°,
∵∠DBG=∠CBA,
∴△DBG∽△CBA,
∴
=(
)2=
,
∵DH=BG,BG=2HG,
∴DG=3HG,
∴
=
,
∴
=
.
| 1 |
| 2 |
| 1 |
| 2 |
∵∠A+∠B+∠C+∠D=360°,
∴3∠B+3∠C=360°,
∴∠B+∠C=120°,
即∠B与∠C的度数和为120°;
(2)证明:∵在△BED和△BEO中
|
∴△BED≌△BEO,
∴∠BDE=∠BOE,
∵∠BCF=
| 1 |
| 2 |
∴∠BCF=
| 1 |
| 2 |
连接OC,
设∠EAF=α,则∠AFE=2∠EAF=2α,
∴∠EFC=180°-∠AFE=180°-2α,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠AOC=180°-∠OAC-∠OCA=180°-2α,
∴∠ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形DBCF是半对角四边形;

(3) 过点O作OM⊥BC于M,
∵四边形DBCF是半对角四边形,
∴∠ABC+∠ACB=120°,
∴∠BAC=60°,
∴∠BCO=2∠BAC=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴BC=2BM=
| 3 |
| 3 |
∵DG⊥OB,
∴∠HGB=∠BAC=60°,
∵∠DBG=∠CBA,
∴△DBG∽△CBA,
∴
| △DBG的面积 |
| △ABC的面积 |
| BD |
| BC |
| 1 |
| 3 |
∵DH=BG,BG=2HG,
∴DG=3HG,
∴
| △BHG的面积 |
| △BDG的面积 |
| 1 |
| 3 |
∴
| △BHG的面积 |
| △ABC的面积 |
| 1 |
| 9 |
看了 有两个内角分别是它们对角的一...的网友还看了以下:
在4*4的方格中,将1至16无重复的填入方格中,使横向和、竖向和、对角线和、中间四数之和以及角上四 2020-04-07 …
AB为一条直线,OC是角AOD的平分线,OE在角BOD内,角DOE=四分之一角BOD,角COE=7 2020-06-05 …
几何体求四边形的度数四边形ABCD中、角A:角B=5:7,角B-角A=角C,角D与角C的差为80度 2020-06-06 …
已知ob平分角aoc,且角二比角三比小四等于二比五比三,求角一,角二,角三,角四度数. 2020-06-18 …
如图所示在三角形abc中,ad垂直于bc于d,ae平分角bac,其中角c大于角的,一,叫c等于六十 2020-06-18 …
细心观察前三个图形,按下述方法找出规律(1)分别求出前面三个图形四角中四个数的积;(2)分别求出前 2020-06-19 …
高一数学问题一个定义域在0到二分之派的角.求,这个角加上四分之派的余玄的十倍跟号二倍再加上20在整 2020-07-15 …
如图所示的一个圆分割成四个扇形,它们的圆心角的度数比为2:3:4:3.(1)求这四个扇形的圆心角的 2020-07-26 …
什么是四分位数?四分位数:将所有数值按大小顺序排列并分成四等份,处于三个分割点位置的得分就是四分位数 2020-11-06 …
我们已经知道三角形的内角和是1800,我们可以用这个知识求出四边形、五边形、六边形内角和的度数,进而 2021-02-01 …