如图，在坡度i=1：3的斜坡AB上立有一电线杆EF，工程师在点A处测得E的仰角为60°，沿斜坡前进20米到达B，此时测得点E的仰角为15°，现要在斜坡AB上找一点P，在P处安装一根拉绳PE来固定电线杆

Question

如图，在坡度i=1：

√(3)的斜坡AB上立有一电线杆EF，工程师在点A处测得E的仰角为60°，沿斜坡前进20米到达B，此时测得点E的仰角为15°，现要在斜坡AB上找一点P，在P处安装一根拉绳PE来固定电线杆，以使EF保持竖直，为使拉绳PE最短，则FP的长度约为（　　）（参考数据：√(2)≈1.414，√(3)≈1.732）

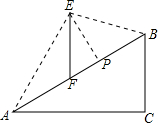
A. 3.7米

B. 3.9米

C. 4.2米

D. 5.7米

Answer 1

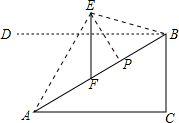作BD∥AC，如右图所示，
∵斜坡AB的坡度i=1：√(3)，
∴tan∠BAC=(1)/(√(3))=(√(3))/(3)，
∴∠BAC=30°，
∵∠EAC=60°，
∴∠EAF=30°，
∵要使点E到AB的距离最短，
∴EP⊥AB于点P，
∴tan∠EAP=(EP)/(AP)，
∴AP=(EP)/(tan30°)，
∵∠EBD=15°，BD∥AC，
∴∠DBA=∠BAC=30°，
∴∠EBP=45°，
∴EP=PB，
∵AP+PB=AB=20米，
∴(EP)/(tan30°)+EP=20，
解得，EP=10√(3)-10，
又∵EF∥BC，∠B=90°-∠BAC=60°，
∴∠EFP=60°，
∵tan∠EFP=(EP)/(PF)，
即tan60°=(10√(3)-10)/(PF)，
解得，PF≈4.2米，
故选C．