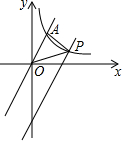
如图，在平面直角坐标系中，直线y=2x与反比例函数y=kx在第一象限内的图象交于点A（m，2），将直线y=2x向下平移后与反比例函数y=kx在第一象限内的图象交于点P，且△POA的面积为2．（1）求k

Question

如图，在平面直角坐标系中，直线y=2x与反比例函数y=(k)/(x)在第一象限内的图象交于点A（m，2），将直线y=2x向下平移后与反比例函数y=(k)/(x)在第一象限内的图象交于点P，且△POA的面积为2．

（1）求k的值．
（2）求平移后的直线的函数解析式．

Answer 1

（1）∵点A（m，2）在直线y=2x，
∴2=2m，
∴m=1，
∴点A（1，2），
∵点A（1，2）在反比例函数y=(k)/(x)上，
∴k=2，
（2）如图，

设平移后的直线与y轴相交于B，过点P作PM⊥OA，BN⊥OA，AC⊥y轴
由（1）知，A（1，2），
∴OA=√(5)，sin∠BON=sin∠AOC=(AC)/(OA)=(√(5))/(5)，
∵S_△POA=(1)/(2)OA×PM=(1)/(2)×√(5)PM=2，
∴PM=(4√(5))/(5)，
∵PM⊥OA，BN⊥OA，
∴PM∥BN，
∵PB∥OA，
∴四边形BPMN是平行四边形，
∴BN=PM=(4√(5))/(5)，
∵sin∠BON=(BN)/(OB)=((4√(5))/(5))/(OB)=(√(5))/(5)，
∴OB=4，
∵PB∥AO，
∴B（0，-4），
∴平移后的直线PB的函数解析式y=2x-4