早教吧作业答案频道 -->数学-->
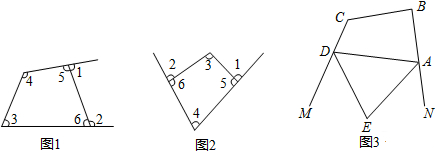
(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;(2)用你发现的结论解决下列问题:如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
题目详情
(1)如图1、2,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
(2)用你发现的结论解决下列问题:
如图3,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

▼优质解答
答案和解析
(1) ∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)答:四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3) ∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=
∠MDA,∠DAE=
∠NAD,
∴∠ADE+∠DAE=
(∠MDA+∠NAD)=
×240°=120°,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)答:四边形的任意两个外角的和等于与它们不相邻的两个内角的和;
(3) ∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°,
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADE+∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
看了 (1)如图1、2,试研究其中...的网友还看了以下:
设四阶矩阵B=1−101000000−101−101,C=2102000034132102,且矩阵 2020-04-12 …
如图,平行四边形ABCD中,AE=CG,DH=BF,连结E,F,G,H,E,则四边形EFHG是?如 2020-05-16 …
用这些英文字母拼词这些英文字母打乱了顺序.一个题目一个词.第一题:r,c,t,a,e,s,r第二题 2020-05-16 …
A、B、C、D、E这五个同学进入足球赛A说:“B第三名,C第五名.”B说:“D第二名,E第四名.” 2020-06-12 …
赛马比赛前,五位观众给A、B、C、D、E五匹赛马预测名次.甲说:“B第三,C第五.”乙说:“E第四 2020-06-15 …
赛马比赛前,五位观众给A、B、C、D、E五匹赛马预测名次.甲说:“B第三,C第五.”乙说:“E第四 2020-07-08 …
设A为主对角线元素均为零的四阶实对称可逆矩阵,E为四阶单位矩阵B=0000000000k0000l 2020-08-02 …
若数列An={an}:a1,aa,…,an(n≥a)满足|ak+1-ak|=1(k=1,a,…,n- 2020-10-31 …
一次唱歌比赛,A.B.C.D.E,五位同学位于前五名,事后有人问他们的名次,他们是这样回答的A说B第 2020-10-31 …
A、B、C、D、E为前四周期元素,且原子序数依次增大A第二周期中一种非金属元素,第一电离能大于相邻元 2020-11-01 …