如图，在Rt△ABC中，∠ACB=90°，以BC为直径作圆，交斜边AB于点E，D为AC的中点．连接DO，DE．则下列结论中不一定正确的是（）A、DO∥ABB、△ADE是等腰三角形

Question

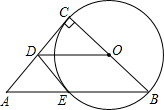如图，在Rt△ABC中，∠ACB=90°，以BC为直径作圆，交斜边AB于点E，D为AC的中点．连接DO，DE．则下列结论中不一定正确的是（　　）

A、DO∥AB

B、△ADE是等腰三角形

C、DE⊥AC

D、DE是⊙O的切线

Answer 1

分析：
连接OE，由OD为三角形ABC的中位线，利用中位线定理得到OD与AB平行，选项A正确；由两直线平行得到两对同位角相等，两对内错角相等，再由OE=OB，利用等边对等角得到一对角相等，等量代换得到一对角相等，再由OC=OE，OD为公共边得到三角形COD与三角形EOD全等，由全等三角形的对应角相等得到∠OED为直角，即OE垂直于DE，可得出DE为圆O的切线，选项D正确；由全等三角形对应角相等得到∠CDO=∠EDO，等量代换得到∠A=∠DEA，即三角形AED为等腰三角形，选项B正确，而DE不一定垂直于AC，故选项C符合题意．

连接OE，∵D为AC中点，O为BC中点，∴OD为△ABC的中位线，∴DO∥AB，选项A正确；∴∠COD=∠B，∠DOE=∠OEB，∠CDO=∠A，∠EDO=∠DEA，∵OE=OB，∴∠OEB=∠B，∴∠COD=∠DOE，在△COD和△EOD中，OC=OE∠COD=∠EODOD=OD，∴△COD≌△EOD（SAS），∴∠OED=∠OCD=90°，∠CDO=∠EDO，∴DE为圆O的切线，选项D正确；∠A=∠DEA，∴△AED为等腰三角形，选项B正确，则不一定正确的为DE⊥AC．故选C
点评：
此题考查了切线的判定，以及全等三角形的判定与性质，熟练掌握切线的判定方法是解本题的关键．