早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面
题目详情
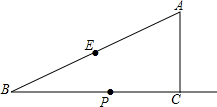
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为___.

▼优质解答
答案和解析
∵∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,
∴AB=4,AE=
AB=2,BC=2
.
①若PA′与AB交于点F,连接A′B,如图1.
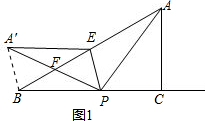
由折叠可得S△A′EP=S△AEP,A′E=AE=2,.
∵点E是AB的中点,
∴S△BEP=S△AEP=
S△ABP.
由题可得S△EFP=
S△ABP,
∴S△EFP=
S△BEP=
S△AEP=
S△A′EP,
∴EF=
BE=BF,PF=
A′P=A′F.
∴四边形A′EPB是平行四边形,
∴BP=A′E=2;
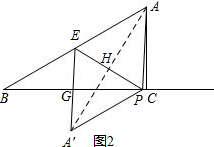
②若EA′与BC交于点G,连接AA′,交EP与H,如图2.
 .
.
同理可得GP=
BP=BG,EG=
EA′=
×2=1.
∵BE=AE,∴EG=
AP=1,
∴AP=2=AC,
∴点P与点C重合,
∴BP=BC=2
.
故答案为2或2
.
∴AB=4,AE=
| 1 |
| 2 |
| 3 |
①若PA′与AB交于点F,连接A′B,如图1.

由折叠可得S△A′EP=S△AEP,A′E=AE=2,.
∵点E是AB的中点,
∴S△BEP=S△AEP=
| 1 |
| 2 |
由题可得S△EFP=
| 1 |
| 4 |
∴S△EFP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形A′EPB是平行四边形,
∴BP=A′E=2;
②若EA′与BC交于点G,连接AA′,交EP与H,如图2.
 .
.同理可得GP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BE=AE,∴EG=
| 1 |
| 2 |
∴AP=2=AC,
∴点P与点C重合,
∴BP=BC=2
| 3 |
故答案为2或2
| 3 |
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
在菱形纸片ABCD中,∠A=60°,将纸片按如图所示的方式折叠,使点A,D分别落在A',D'处,且 2020-05-16 …
菱形纸片ABCD中,角A=60°,将纸片折叠,点A,D分别落在A' D'处,且A' D'经过B E 2020-05-16 …
设a,b,c为满足a+b+c=1的正实数,证明:a3√1+b-c+b3√1+c-a+c3√1+a- 2020-05-16 …
己知:Rt△OAB在直角坐标系中的位置如图所示,点B的坐标为(4,2),P为OB的中点,点C为折线 2020-07-20 …
(a+b-c)(a+b+c)为什么可以(a+b)的平方-c的平方啊?不是只有a+b+c才能变成(a 2020-07-31 …
如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、 2020-11-01 …
直角三角形ABC中,BC=2,AC=6,依下列的步骤抄作折纸.(A)将A,C两点重合(B)DE为折痕 2020-11-06 …
直角三角形ABC中,BC=2,AC=6,依下列的步骤抄作折纸.(A)将A,C两点重合(B)DE为折痕 2020-12-02 …
数学方面的.1.将长度为2N(N≥4,N是自然数)的一根铁丝折成各边的长均为整数的三角数,记(A,B 2021-01-22 …