早教吧作业答案频道 -->数学-->
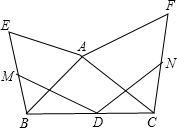
如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.
题目详情
如图,D为△ABC的边BC的中点,△ABE,△ACF均为正三角形,M,N分别为BE,CF的中点,求∠MDN的度数.

▼优质解答
答案和解析
连接BF、CE,如图所示: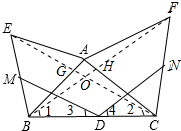
∵△ABE,△ACF均为正三角形,
∴∠BAE=∠CAF=60°,AE=AB,AC=AF,
∴∠EAC=∠BAF,
在△EAC和△BAF中,
,
∴△EAC≌△BAF(SAS),
∴∠AEC=∠ABF,
∵∠AME=∠BMC,
∴∠BOG=∠BAE=60°,
∴∠1+∠2=∠BOM=60°,
∵M,N分别为BE,CF的中点,D为△ABC的边BC的中点,
∴DE是△BCE的中位线,DN是△BCF的中位线,
∴DM∥CE,DN∥BF,
∴∠3=∠2,∠4=∠1,
∴∠3+∠4=∠1+∠2=60°,
∴∠MDN=180°-60°=120°.

∵△ABE,△ACF均为正三角形,
∴∠BAE=∠CAF=60°,AE=AB,AC=AF,
∴∠EAC=∠BAF,
在△EAC和△BAF中,
|
∴△EAC≌△BAF(SAS),
∴∠AEC=∠ABF,
∵∠AME=∠BMC,
∴∠BOG=∠BAE=60°,
∴∠1+∠2=∠BOM=60°,
∵M,N分别为BE,CF的中点,D为△ABC的边BC的中点,
∴DE是△BCE的中位线,DN是△BCF的中位线,
∴DM∥CE,DN∥BF,
∴∠3=∠2,∠4=∠1,
∴∠3+∠4=∠1+∠2=60°,
∴∠MDN=180°-60°=120°.
看了 如图,D为△ABC的边BC的...的网友还看了以下:
一次数学测验中得a分的有5人,得b分的有8人,得c分的有12人,则这次测验的平均成绩是 2020-03-30 …
已知二次函数f(x)=4x2-2p(p-2)-2p2-p+1在区间[-1,1]内至少存在一点c,使 2020-05-13 …
已知椭圆方程为x^2/a^2+y^2/b^2=1(a>b>0),过椭圆焦点F(c,0)的直线与椭圆 2020-05-23 …
f(x)=x^2-bx+c,且f(1+x)=f(1-x),f(0)=3,求f(b^x)与f(c^x 2020-06-04 …
设A={a,b,c}b={-1,0,1},满足f(a)+f(b)+f(c)=0的映射f的个数 2020-06-05 …
小学五年级下册UNIT3人教版的F部分的英语作文第47急好的有赏NOWuseyournoutesa 2020-06-07 …
现有A,B,C,D,E,F,G七种短周期主族元素,原子序数依次增大.已知A与D,C与F分别同主族, 2020-07-07 …
以知M={a,b,c},N={-3,0,3},则满足条件f(a)+f(b)+f(c)=0的映射f: 2020-07-30 …
一个人买了D元C分的商品,交给营业员20元,营业员误看成C元D分,于是找给顾客4.88元,那么按正确 2020-12-10 …
已知b分之a=d分之c=f分之e=...=n分之m,且b+d+f+...+n不等于0,求证b+d+f 2020-12-17 …