早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A的坐标为(-6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.(2)过点A作AD⊥x轴,
题目详情
在平面直角坐标系中,点A的坐标为(-6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
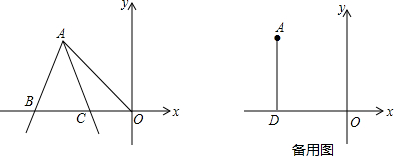
(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
▼优质解答
答案和解析
 (1)∵AB=AC,∠BAC=45°,
(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)设OM=x.
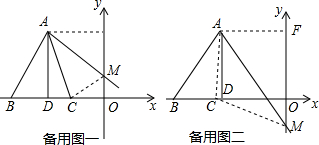
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°,
可知:∠BAD=∠MAF;
∴在△BAD和△MAF中,
,
∴△BAD≌△MAF.
∴BD=FM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
 (1)∵AB=AC,∠BAC=45°,
(1)∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=
| 1 |
| 2 |
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°,
可知:∠BAD=∠MAF;
∴在△BAD和△MAF中,
|
∴△BAD≌△MAF.
∴BD=FM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
看了 在平面直角坐标系中,点A的坐...的网友还看了以下:
已知a(x的平方+x-c)+b(2x的平方-x-2)=7x的平方+4x+3问a,b,c的值各是多少 2020-05-16 …
已知a、b、c是△ABC的三条边的长,且关于x的方程(c-b)x²+2(b-a)x+(a-b)=0 2020-06-06 …
制造和销售每一个包的成本为C元.如果每一个书包的售价为X元,售出书包的数量由:n=a/(x-c)+ 2020-06-14 …
以知a.b满足(a-b)的平方+|ab+6|=0(1)如果X=2a+3b+3,求此时X的值;(2. 2020-07-08 …
某物理学习小组通过实验,得到了a,b,c三个实心体的质量与体积的关系如图所示,分析图象可知()A. 2020-07-20 …
制作和销售每一个背包的成本为C元,如果每个背包的售价为x元,售出背包数由n=a/(x-c)+b(1 2020-07-26 …
下列情形时,如果a>0,抛物线y=a*x^2+b*x+c的顶点在顶点在什么?(1)方程a*x^2+ 2020-07-29 …
刚刚看到的贴吧的1、若abc=1,求证:(1/ab+a+a)+(1/bc+b+1)+(1/ac+c+ 2020-10-31 …
设实数a.b.c满足a≥b≥c,且√(1/a^2+1/b^2+1/c^2)=|1/a+1/b+1/c 2020-12-31 …
f(x)的原函数是lnx,那么xf(x)的原函数是?A2x²lnxx²C,B.2x²lnxf(x)的 2021-02-09 …