早教吧作业答案频道 -->数学-->
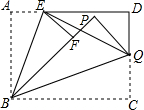
如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把∠A沿BE折叠,使点A落在F处,点Q是CD上一点,将∠C沿BQ折叠,点C恰好落在直线BF上,若∠BQE=45°,则AE=.
题目详情
如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把∠A沿BE折叠,使点A落在F处,点Q是CD上一点,将∠C沿BQ折叠,点C恰好落在直线BF上,若∠BQE=45°,则AE=___.

▼优质解答
答案和解析
由翻折的性质可知:∠ABE=∠FBE,∠CBQ=∠PBQ.
∴∠EBQ=
∠ABC=
×90°=45°.
∴∠EBQ=∠BQE=45°.
∴BE=EQ,∠BEQ=90°.
∴∠DEQ+∠AEB=90°.
又∵∠AEB+∠ABE=90°,
∴∠DEQ=∠ABE.
在△AEB和△DQE中,
,
∴△AEB≌△DQE.
∴DE=AB=4.
∴AE=AD-DE=6-4=2.
故答案为:2.
∴∠EBQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EBQ=∠BQE=45°.
∴BE=EQ,∠BEQ=90°.
∴∠DEQ+∠AEB=90°.
又∵∠AEB+∠ABE=90°,
∴∠DEQ=∠ABE.
在△AEB和△DQE中,
|
∴△AEB≌△DQE.
∴DE=AB=4.
∴AE=AD-DE=6-4=2.
故答案为:2.
看了 如图,在矩形ABCD中,AB...的网友还看了以下:
如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长 2020-05-14 …
如图,长方形纸片abcd,点e.f分别在边ab.cd上,连接ef.将角bef对折,点b落在直线ef 2020-05-16 …
在平面直角坐标系中,平行四边形ABCD的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2),将 2020-06-06 …
在平面直角坐标系中,直线y=−43x+8与x轴、y轴分别交于A、B两点,把直线y=−43x+8沿过 2020-06-12 …
如图长方形纸片ABCD,点E,F如图,长方形纸片ABCD,点E,F分别在AB,CD上,连接EF.将 2020-07-21 …
(2014•牡丹江)如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿 2020-08-01 …
1.已知等腰直角三角形ABC中,∠B=90°,AC,BC的中点分别是D,E,沿DE把该三角形折成直 2020-08-02 …
如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长 2020-08-03 …
直线Y=-2X+10与X轴,Y轴分别交于A,B两点,把三角形AOB沿AB翻折,点oO落在C处,则点C 2020-11-03 …
已知直线y=-x+12与x轴交于点A与y轴交于点B.将三角形D为x轴上一点E为直线上一点,将三角形A 2021-01-10 …