早教吧作业答案频道 -->数学-->
在正方形ABCD中,E为边CD上一点,连接BE.(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;
题目详情
在正方形ABCD中,E为边CD上一点,连接BE.
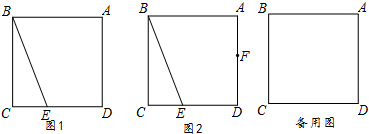
(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;
(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;
(3)在(2)的条件下,若点E为边CD的三等分点,且CE<DE,请写出求cos∠FED的思路.(可以不写出计算结果).
(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;
(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;
(3)在(2)的条件下,若点E为边CD的三等分点,且CE<DE,请写出求cos∠FED的思路.(可以不写出计算结果).

▼优质解答
答案和解析
(1)补全图形,如图1所示,
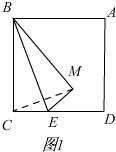
∠ABF与∠CBE的数量关系为:∠ABF+CBE=45°,
证明:如图2,
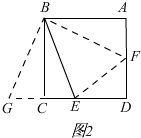
连接BF,EF,延长DC到G,使CG=AF,连接BG,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCD=∠ABC=90°,
∴△BAF≌△BCG,
∴BF=BG,∠ABF=∠CBG,
∵AF+CE=EF,
∴EF=GE,
∴△BEF≌△BEG,
∴∠FBE=∠GBE=∠ABF+∠CBE,
∴∠ABF+∠CBE=45°.
(3) 设正方形的边长为3a,AF=x,
∵点E是CD三等分点
∴EF=CG+CE=x+a,DE=2a,DF=3a-x,
在Rt△DEF中,EF2=DF2+DE2,
∴(x+a)2=(3a-x)2+(2a)2,
∴x=
a,
∴EF=x+a=
a+a=
,
∴cos∠FED=
=
=
.

∠ABF与∠CBE的数量关系为:∠ABF+CBE=45°,
证明:如图2,

连接BF,EF,延长DC到G,使CG=AF,连接BG,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCD=∠ABC=90°,
∴△BAF≌△BCG,
∴BF=BG,∠ABF=∠CBG,
∵AF+CE=EF,
∴EF=GE,
∴△BEF≌△BEG,
∴∠FBE=∠GBE=∠ABF+∠CBE,
∴∠ABF+∠CBE=45°.
(3) 设正方形的边长为3a,AF=x,
∵点E是CD三等分点
∴EF=CG+CE=x+a,DE=2a,DF=3a-x,
在Rt△DEF中,EF2=DF2+DE2,
∴(x+a)2=(3a-x)2+(2a)2,
∴x=
| 3 |
| 2 |
∴EF=x+a=
| 3 |
| 2 |
| 5 |
| 2 |
∴cos∠FED=
| DE |
| EF |
| 2a | ||
|
| 4 |
| 5 |
看了 在正方形ABCD中,E为边C...的网友还看了以下:
a是b的倍数,c是a的倍数(a、c不相同),下列判断错误的是()A、a与b的和也一定是b的倍数B、a 2020-03-30 …
a=x^2-y+1,b=y^2-z+1,c=z^2-x+1,则A、a、b、c三个数中至少一个为0B 2020-04-05 …
c为任意不为0的自然数,下列说法中不正确的是[]A.c是1的倍数B.c不是奇数就是偶数C.c不是质 2020-04-09 …
实数a,b,c是图象连续不断的函数y=f(x)定义域中的三个数,且满足a<b<c,f(a)f(b) 2020-04-09 …
一个奇数(),结果是偶数a.乘5,b.加1,c.减2非零自然数按因数的个数可以分为()a.质数和合 2020-05-15 …
关于正负数,绝对值a,c为小于0的数,即负数b大于0,即正数c小于aa+b的绝对值+b-c的绝对值 2020-05-24 …
一个三位数A,它的百位数字是a,十位数字是b,个位数字是c,且a-c>1,ac不等于0(1)把A的 2020-07-29 …
a,b,c,d都是不同的质数.甲数=a*b*c,乙数=a*b*c*d,则().a.甲是乙的倍数b. 2020-07-31 …
在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、b满足|a+2|+(c-7 2020-11-19 …
如图:在数轴上点A表示数a,点B表示数b,点C表示数c,b是最大的负整数,且a、c满足|a+3|+( 2020-11-20 …