如图的矩形ABCD中，E为.AB的中点，有一圆过C、D、E三点，且此圆分别与.AD、.BC相交于P、Q两点．甲、乙两人想找到此圆的圆心O，其作法如下：（甲）作∠DEC的角平分线L，作.DE的中垂线，交L

Question

如图的矩形ABCD中，E为

.

AB

的中点，有一圆过C、D、E三点，且此圆分别与

.

AD

、

.

BC

相交于P、Q两点．甲、乙两人想找到此圆的圆心O，其作法如下：
（甲） 作∠DEC的角平分线L，作

.

DE

的中垂线，交L于O点，则O即为所求；
（乙） 连接

.

PC

、

.

QD

，两线段交于一点O，则O即为所求
对于甲、乙两人的作法，下列判断何者正确？（　　）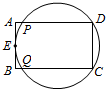

A. 两人皆正确

B. 两人皆错误

C. 甲正确，乙错误

D. 甲错误，乙正确

Answer 1

甲，∵

.

ED

=

.

EC

，
∴△DEC为等腰三角形，
∴L为

.

CD

之中垂线，
∴O为两中垂线之交点，
即O为△CDE的外心，
∴O为此圆圆心．
乙，∵∠ADC=90°，∠DCB=90°，
∴

.

PC

、

.

QD

为此圆直径，
∴

.

PC

与

.

QD

的交点O为此圆圆心，因此甲、乙两人皆正确．
故选：A．