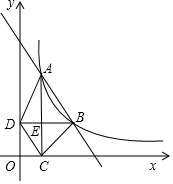
如图，在平面直角坐标系中，函数y=kx（x>0，k是常数）的图象经过A（2，6），B（m，n），其中m>2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，AC与BD交于点E，连结AD，DC，CB．

Question

如图，在平面直角坐标系中，函数y=(k)/(x)（x>0，k是常数）的图象经过A（2，6），B（m，n），其中m>2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，AC与BD交于点E，连结AD，DC，CB．

（1）若△ABD的面积为3，求k的值和直线AB的解析式；
（2）求证：(DE)/(CE)=(BE)/(AE)；
（3）若AD∥BC，求点B的坐标．

Answer 1

（1）∵函数y=(k)/(x)（x>0，k是常数）的图象经过A（2，6），
∴k=2×6=12，
∵B（m，n），其中m>2．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，
∴mn=12①，BD=m，AE=6-n，
∵△ABD的面积为3，
∴(1)/(2)BD•AE=3，
∴(1)/(2)m（6-n）=3②，
联立①②得，m=3，n=4，
∴B（3，4）；
设直线AB的解析式为y=kx+b（k≠0），
则

2k+b=6

3k+b=4

，
∴

k=-2

b=10

，
∴直线AB的解析式为y=-2x+10

（2）∵A（2，6），B（m，n），
∴BE=m-2，CE=n，DE=2，AE=6-n，
∴DE•AE=2（6-n）=12-2n，
BE•CE=n（m-2）=mn-2n=12-2n，
∴DE•AE=BE•CE，
∴(DE)/(CE)=(BE)/(AE)

（3）由（2）知，(DE)/(CE)=(BE)/(AE)，
∵∠AEB=∠DEC=90°，
∴△DEC∽△BEA，
∴∠CDE=∠ABE
∴AB∥CD，
∵AD∥BC，
∴四边形ADCB是平行四边形．
又∵AC⊥BD，
∴四边形ADCB是菱形，
∴DE=BE，CE=AE．
∴B（4，3）．