早教吧作业答案频道 -->数学-->
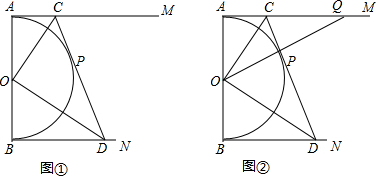
如图①,半圆O的直径AB=6,AM和BN是它的两条切线,CP与半圆O相切于点P,并于AM,BN分别相交于C,D两点.(1)请直接写出∠COD的度数;(2)求AC•BD的值;(3)如图②,连接OP并延长交AM于点Q
题目详情
如图①,半圆O的直径AB=6,AM和BN是它的两条切线,CP与半圆O相切于点P,并于AM,BN分别相交于C,D两点.
(1)请直接写出∠COD的度数;
(2)求AC•BD的值;
(3)如图②,连接OP并延长交AM于点Q,连接DQ,试判断△PQD能否与△ACO相似?若能相似,请求AC:BD的值;若不能相似,请说明理由.
(1)请直接写出∠COD的度数;
(2)求AC•BD的值;
(3)如图②,连接OP并延长交AM于点Q,连接DQ,试判断△PQD能否与△ACO相似?若能相似,请求AC:BD的值;若不能相似,请说明理由.

▼优质解答
答案和解析
(1)∠COD=90°.
理由:如图①中,∵AB是直径,AM、BN是切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵CA、CP是切线,
∴∠ACO=∠OCP,同理∠ODP=∠ODB,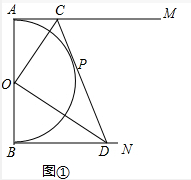
∵∠ACD+∠BDC=180°,
∴2∠OCD+2∠ODC=180°,
∴∠OCD+∠ODC=90°,
∴∠COD=90°.
(2)如图①中,∵AB是直径,AM、BN是切线,
∴∠A=∠B=90°,
∴∠ACO+∠AOC=90°,
∵∠COD=90°,
∴∠BOD+∠AOC=90°,
∴∠ACO=∠BOD,
∴RT△AOC∽RT△BDO,
∴
=
,
即AC•BD=AO•BO,
∵AB=6,
∴AO=BO=3,
∴AC•BD=9.
(3)△PQD能与△ACQ相似.
∵CA、CP是 O切线,
∴AC=CP,∠1=∠2,
∵DB、DP是 O切线,
∴DB=DP,∠B=∠OPD=90°,OD=OD,
∴RT△ODB≌RT△ODP,
∴∠3=∠4,
①如图②中,当△PQD∽△ACO时,∠5=∠1,
∵∠ACO=∠BOD,即∠1=∠3,
∴∠5=∠4,
∴DQ=DO,
∴∠PDO=∠PDQ,
∴△DCQ≌△DCO,
∴∠DCQ=∠2,
∵∠1+∠2+∠DCQ=180°,
∴∠1=60°=∠3,
在RT△ACO,RT△BDO中,分别求得AC=
,BD=3
,
∴AC:BD=1:3.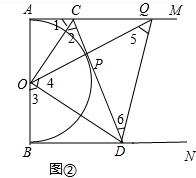
②如图②中,当△PQD∽△AOC时,∠6=∠1,
∵∠2=∠1,
∴∠6=∠2,
∴CO∥QD,
∴∠1=∠CQD,
∴∠6=∠CQD,
∴CQ=CD,
∵S△CDQ=
•CD•PQ=
•CQ•AB,
∴PQ=AB=6,
∵CO∥QD,
∴
=
,即
=
,
∴AC:BD=1:2
理由:如图①中,∵AB是直径,AM、BN是切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵CA、CP是切线,
∴∠ACO=∠OCP,同理∠ODP=∠ODB,

∵∠ACD+∠BDC=180°,
∴2∠OCD+2∠ODC=180°,
∴∠OCD+∠ODC=90°,
∴∠COD=90°.
(2)如图①中,∵AB是直径,AM、BN是切线,
∴∠A=∠B=90°,
∴∠ACO+∠AOC=90°,
∵∠COD=90°,
∴∠BOD+∠AOC=90°,
∴∠ACO=∠BOD,
∴RT△AOC∽RT△BDO,
∴
| AC |
| BO |
| AO |
| BD |
即AC•BD=AO•BO,
∵AB=6,
∴AO=BO=3,
∴AC•BD=9.
(3)△PQD能与△ACQ相似.
∵CA、CP是 O切线,
∴AC=CP,∠1=∠2,
∵DB、DP是 O切线,
∴DB=DP,∠B=∠OPD=90°,OD=OD,
∴RT△ODB≌RT△ODP,
∴∠3=∠4,
①如图②中,当△PQD∽△ACO时,∠5=∠1,
∵∠ACO=∠BOD,即∠1=∠3,
∴∠5=∠4,
∴DQ=DO,
∴∠PDO=∠PDQ,
∴△DCQ≌△DCO,
∴∠DCQ=∠2,
∵∠1+∠2+∠DCQ=180°,
∴∠1=60°=∠3,
在RT△ACO,RT△BDO中,分别求得AC=
| 3 |
| 3 |
∴AC:BD=1:3.

②如图②中,当△PQD∽△AOC时,∠6=∠1,
∵∠2=∠1,
∴∠6=∠2,
∴CO∥QD,
∴∠1=∠CQD,
∴∠6=∠CQD,
∴CQ=CD,
∵S△CDQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴PQ=AB=6,
∵CO∥QD,
∴
| PC |
| PD |
| PO |
| PQ |
| AC |
| BD |
| 3 |
| 6 |
∴AC:BD=1:2
看了 如图①,半圆O的直径AB=6...的网友还看了以下:
垂径定理的应用已知A、B都是⊙O的玄,且AB//CD,求证:弧AC=弧BD 2020-03-30 …
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=50°,∠DCF=4 2020-04-25 …
(2004•香坊区一模)如图,⊙O是Rt△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=0 2020-05-13 …
已知:如图,在直角坐标系中,直角三角形OAB,O为坐标原点,AB=1,OB=3,将△OAB绕着A点 2020-05-13 …
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD1.A,B,C,D,P是⊙O上的五个 2020-05-20 …
如图,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O上一点,且PA=PB,延长BO分别与⊙O 2020-06-15 …
如图,A,P,B,C是⊙O上的四点,∠APC=∠BPC=60°猜想pa pb pc三者间的数量关系 2020-06-27 …
如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别是 2020-07-21 …
如图所示,OD⊥BC,垂足为D,连接OB,下列说法正确的是()①线段OB是O,B两点间的距离②线段 2020-07-25 …
如图,⊙O是以坐标原点O为圆心、半径为25的圆,P(a,b)为⊙O上一点,若a、b都是整数,那么符 2020-07-26 …