早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,E是BC边的中点,DE⊥AC,垂足为点F,连接BF,下列四个结论:①△CEF∽△ACD;②AFCF=2;③sin∠CAD=12;④AB=BF.其中正确的结论有
题目详情
如图,在矩形ABCD中,E是BC边的中点,DE⊥AC,垂足为点F,连接BF,下列四个结论:①△CEF∽△ACD;②
=2;③sin∠CAD=
;④AB=BF.其中正确的结论有___(写出所有正确结论的序号).
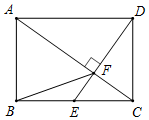
| AF |
| CF |
| 1 |
| 2 |

▼优质解答
答案和解析
过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ADC=90°,AD=BC,BE⊥AC于点F,
∴∠DAC=∠ECF,∠ADC=∠CFE=90°,
∴△CEF∽△ADC,故①正确;
∵AD∥BC,
∴△CEF∽△ADF,
∴
=
,
∵CE=
BC=
AD,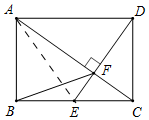
∴
=
=2,
∴AF=2CE,故②正确,
设CF=a,AF=2a,由DF2=AF•CF=2a2,得DF=
a,AD=
=
a
∴sinCAD=
=
=
,故③错误.
连接AE,∵∠ABE+∠AFE=90°,
∴A、B、E、F四点共圆,
∴∠AFB=∠AEB,
∵AB=CD,BE=EC,∠CDE,
∴△ABE≌△CDE,
∴∠AEB=∠CED,
∵∠BAF+∠BEF=180°,∠BEF+∠CED=180°,
∴∠BAF=∠CED,
∴∠BAF=∠BFA,
∴BA=BF,故④正确.
故答案为①②④.
∵四边形ABCD是矩形,
∴AD∥BC,∠ADC=90°,AD=BC,BE⊥AC于点F,
∴∠DAC=∠ECF,∠ADC=∠CFE=90°,
∴△CEF∽△ADC,故①正确;
∵AD∥BC,
∴△CEF∽△ADF,
∴
| CE |
| AD |
| CF |
| AF |
∵CE=
| 1 |
| 2 |
| 1 |
| 2 |

∴
| AF |
| FC |
| AD |
| CE |
∴AF=2CE,故②正确,
设CF=a,AF=2a,由DF2=AF•CF=2a2,得DF=
| 2 |
| AF2+DF2 |
| 6 |
∴sinCAD=
| DF |
| AD |
| ||
|
| ||
| 3 |
连接AE,∵∠ABE+∠AFE=90°,
∴A、B、E、F四点共圆,
∴∠AFB=∠AEB,
∵AB=CD,BE=EC,∠CDE,
∴△ABE≌△CDE,
∴∠AEB=∠CED,
∵∠BAF+∠BEF=180°,∠BEF+∠CED=180°,
∴∠BAF=∠CED,
∴∠BAF=∠BFA,
∴BA=BF,故④正确.
故答案为①②④.
看了 如图,在矩形ABCD中,E是...的网友还看了以下:
下列结论中正确的是A圆的切线垂直于半径B垂直于切线的直线必经过圆心下列结论中正确的是A圆的切线垂直 2020-06-08 …
如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是()A.点B到AC的垂线段 2020-06-15 …
(2014•安徽)如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段A 2020-06-17 …
辩论中如何驳斥不知足常乐抛出的关于只有不知足才能促进进步、知足会导致停滞不前的论点?即如何反驳:提 2020-06-21 …
如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下 2020-07-20 …
如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、 2020-11-02 …
(2009•衡阳)如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=45,则下列结 2020-11-12 …
(2013•保定模拟)如图:AB是AB所对的弦,AB的中垂线CD分别交AB于C,交AB于D,AD的中 2020-11-12 …
如图,在△ABC中,CD⊥AB,垂足为D,AE分别交BC、CD于E、F,EH⊥AB,垂足为H,且四边 2020-12-23 …
相对论中说:一个人在一辆接近光速飞驰的火车上点燃一个火把,让它射到和它垂直的一面贴在车顶的镜子上…… 2020-12-23 …