早教吧作业答案频道 -->数学-->
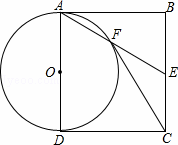
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.(1)求证:CF与⊙O相切;(2)若AD=2,F为AE的中点,求AB的长.
题目详情
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.
▼优质解答
答案和解析
(1)证明:如图所示:连接OF、OC, ∵四边形ABCD是矩形, ∴AD∥BC,AD=BC,∠ADC=90°, ∵E为BC边中点,AO=DO, ∴AO=AD,EC=BC, ∴AO=EC,AO∥EC, ∴四边形OAEC是平行四边形, ∴AE∥OC, ∴∠DOC=∠OAF,∠FOC=∠OFA, ∵OA=OF, ∴∠OAF=∠OFA, ∴∠DOC=∠FOC, ∵在△ODC和△OFC中 , ∴△ODC≌△OFC(SAS), ∴∠OFC=∠ODC=90°, ∴OF⊥CF, ∴CF与⊙O相切; (2)如图所示:连接DE, ∵AO=DO,AF=EF,AD=2, ∴DE=20F=2, ∵E是BC的中点, ∴EC=1, 在Rt△DCE中,由勾股定理得: DC===, ∴AB=CD=.
看了 如图,四边形ABCD为矩形,...的网友还看了以下:
集合A非空,有A*B=A*C 求证:B=C 2020-05-16 …
已知Asec(a)-Ctan(a)=d,Bsec(a)+Dtan(a)=c求证:(A^2)+(B^ 2020-06-13 …
数学厉害的进来1求证a²+3b²≥2b(a+b)2,求证a²+b²+2≥2a+2b3,已知a≠2, 2020-07-09 …
为什么双曲线右支上的点到左焦点F1的最短距离是a+c?求证明~但是我不知道这个结论是否具有普遍性还 2020-07-20 …
如图,在△ABC和△A'B'C'中,AB/A'B'=BC/B'C'=AC/A'C'求证△ABC∽△ 2020-07-21 …
在三角形ABC中,若三内角ABC满足2B=A+C,对应三边abc也满足2b=a+c,求证三角形是等 2020-07-22 …
正余弦定理的综合应用在△ABC中,若2b=a+c,求证:2cos((A+C)/2))=cos((A 2020-08-02 …
已知,如图,△ABC和△A'B'C'中,∠BAC=∠B'A'C',∠B=∠B',AD,A'D分别∠B 2020-11-01 …
求一道数学题解(急)1/a+1/b+1/c=1/a+b+c,求证啊a+b=0或b+c=0或a+c=0 2020-11-05 …
如图所示,在三角形ABC和三角形A'B'C'中,AD、A'C'分别是BC、B'C'上的中线,且AB= 2020-12-05 …