早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:(1)∠BGC=90°+12∠BAC;(2)∠1=∠2.
题目详情
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:
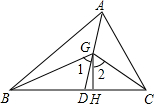
(1)∠BGC=90°+
∠BAC;
(2)∠1=∠2.

(1)∠BGC=90°+
| 1 |
| 2 |
(2)∠1=∠2.
▼优质解答
答案和解析
(1)由三角形内角和定理可知:∠ABC+∠ACB=180°-∠BAC,
∵BG,CG分别平分∠ABC,∠ACB,
∠GBC=
∠ABC,∠GCB=
∠ACB
∴∠GBC+∠GCB=
(∠ABC+∠ACB)=
(180°-∠BAC)=90°-
∠BAC
∴∠BGC=180°-(∠GBC+∠GCB)=180°-
(∠ABC+∠ACB)=90°+
∠BAC;
(2)∵AD是它的角平分线,
∴∠BAD=∠CAD
∴∠1=∠BAD+∠ABG,
∵GH⊥BC,
∴∠GHC=90°
∴∠2=90°-∠GCH
=90°-
∠ACB
=90°-
(180°-∠DAC-∠ADC)
=
∠DAC+
∠ADC
∵∠ADC=∠ABC+∠BAD,
∴
∠ADC=
∠ABC+∠
∠BAD
=∠ABG+
∠BAD,
∴∠2=
∠DAC+
∠ADC
=
∠BAD+
∠BAD+∠ABG
=∠BAD+∠ABG,
∴∠1=∠2,
∵BG,CG分别平分∠ABC,∠ACB,
∠GBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GBC+∠GCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BGC=180°-(∠GBC+∠GCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵AD是它的角平分线,
∴∠BAD=∠CAD
∴∠1=∠BAD+∠ABG,
∵GH⊥BC,
∴∠GHC=90°
∴∠2=90°-∠GCH
=90°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC=∠ABC+∠BAD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=∠ABG+
| 1 |
| 2 |
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=∠BAD+∠ABG,
∴∠1=∠2,
看了 如图,在△ABC中,AD是它...的网友还看了以下:
一道六年级英语单选题(急救~)1.Whatyoudidmademe.A.excitingB.hap 2020-04-26 …
设a=lge,b=(lge)^2,c=lg(e开平方),a,b,c的大小我算得是a=b开平方=2c 2020-05-13 …
数学向量证明题试证明;向量(a·b)b-(b·c)a与c 垂直.打错了。是(a·c)b 2020-05-16 …
是求椭圆离心率的一道题,化简完得到的b与c的关系是√6×c²=b√b²+c²,怎么化简得到的b²= 2020-06-03 …
条件概率问题,已知P(A),P(B|A),P(C|A),能否求得P(C|A,B)?写错了,是已知P 2020-06-13 …
A为3维行向量,B为3维列向量,A,B满足A*B=2,则矩阵B*A的非零特征值为答案的解法是设C= 2020-06-20 …
组织含水率的计算(植物)组织块鲜重A克,晾干后重量B克,经105℃烘干至恒重,重量C克,求晾干组织 2020-07-06 …
如果a>b,则a+b>b+c,在这个命题中涉及的公理和定理是?打错了是A+C>B+C 2020-07-30 …
以下选项中不属于字符常量的是A:'C'B:"C"C:'\xCC0'D:'\072' 2020-11-07 …
初一数学题A、B、C是一条公路上的三个村庄,AB=100km,AC=40km,现在计划在AB上造一个 2020-11-22 …