早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.(1)求证:AB是半圆O所在圆的切线;(2)若cos∠ABC=23,AB=12,求半圆O所在圆的半径.
题目详情
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
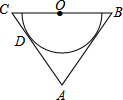
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=
,AB=12,求半圆O所在圆的半径.

(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=
| 2 |
| 3 |
▼优质解答
答案和解析
(1)证明:如图1
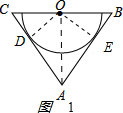 ,
,
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=
,AB=12,得
OB=8.
由勾股定理,得
AO=
=4
.
由三角形的面积,得
S△AOB=
AB•OE=
OB•AO,
OE=
=
,
半圆O所在圆的半径是
.
 ,
,作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=
| 2 |
| 3 |
OB=8.
由勾股定理,得
AO=
| AB2-OB2 |
| 5 |
由三角形的面积,得
S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
OE=
| OB•AO |
| AB |
8
| ||
| 3 |
半圆O所在圆的半径是
8
| ||
| 3 |
看了 如图,在△ABC中,AB=A...的网友还看了以下:
中心在原点,焦点在x轴上的双曲线C1的离心率为e,直线l与双曲线C1交于A,B两点,线段AB中点M 2020-05-13 …
1.已知线段AB=100毫米,点M在AB上,MB=52毫米,P是AM的中点,求MP的长2.AB=2 2020-05-13 …
已知双曲线为x²/4-y²/12=1,A(1,0)为定点,过右焦点F的直线与双曲线右支交于B、C两 2020-05-15 …
已知向量OA=(K,12),向量OB=(4,5),向量OC=(-5,10),且A,B,C三点共线. 2020-05-15 …
直线4x+3y=12于坐标轴交与AB两点,圆o的圆心在原点上与线段AB有两个交点,直线4x+3y= 2020-06-10 …
我们知道,“两点之间线段最短”,“直线外一点与直线上各点连线的所有线段中,垂线段最短”.在此基础上 2020-06-17 …
怎么根据晨昏线与纬线经线圈的切点位置判断0点6点12点18点最好有图 2020-07-28 …
已知椭圆:x^2/24+y^2/16=1.直线L:x/12+y/8=1,P是L上一点,射线OP交椭 2020-07-31 …
(本小题满分12分)已知两条直线,点.直线过点,且与直线垂直,求直线的方程;若直线与直线平行,求的值 2020-11-01 …
在图中,a、b分别在两条日期分界线上,OMP为晨昏线,M为弧OP的中点,又是该线纬度最高点,O位于东 2020-12-05 …