早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为.
题目详情
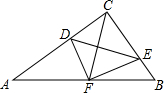
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为___.

▼优质解答
答案和解析
 由折叠可得,∠DCE=∠DFE=90°,
由折叠可得,∠DCE=∠DFE=90°,
∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF=
AB=5,
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD=
,
故答案为:
.
 由折叠可得,∠DCE=∠DFE=90°,
由折叠可得,∠DCE=∠DFE=90°,∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF=
| 1 |
| 2 |
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD=
| 25 |
| 8 |
故答案为:
| 25 |
| 8 |
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
读图--三幅经纬网图,完成3-4题.下列关于方位的说法正确的是()A.a点在b点的正北方向B.c点 2020-05-13 …
如图所示,把一个长方形纸片沿EF折叠后,点D,C落在D",C"的位置.若∠DEF=65°,则∠AE 2020-05-13 …
光速是最快的速度光速D点到E点距离为100,A为观察1B为观察2,c是运动1,c1在c里,在D点时 2020-05-15 …
2013年9月9日,WTA官网公布最新一期网球女单选手世界排名,我国女选手李娜位居第5位,如图,李 2020-06-12 …
2013年9月9日,WTA官网公布最新一期网球女单选手世界排名,我国女选手李娜位居第5位,如图所示 2020-06-12 …
如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( ) A 2020-06-27 …
(2010•岳阳)如图为伽利略理想实验示意图,实验过程中,小球()A.在b点的速度最小B.在a点的 2020-07-15 …
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线顶点A的坐标;(2)设 2020-07-30 …
(2012•宜宾)如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线顶点A 2020-11-12 …
22.发生地震时,如下做法正确的是:A如在教室内,迅速钻到桌子下B如在教室在迅速从楼梯跑出到操场集合 2020-12-04 …