早教吧作业答案频道 -->数学-->
在△ABC中,以AB为斜边,作直角△ABD,使点D落在△ABC内,∠ADB=90°.(1)如图1,若AB=AC,∠BAD=30°,AD=63,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;(2)如图2,若AB=AC,把△ABD绕
题目详情
在△ABC中,以AB为斜边,作直角△ABD,使点D落在△ABC内,∠ADB=90°.
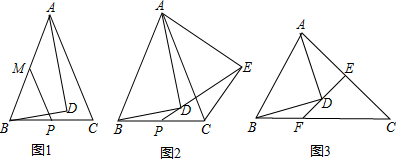
(1)如图1,若AB=AC,∠BAD=30°,AD=6
,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP
(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).

(1)如图1,若AB=AC,∠BAD=30°,AD=6
| 3 |
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP
(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).
▼优质解答
答案和解析
(1) ∵∠ADB=90°,∠BAD=30°,AD=6
,
∴cos∠BAD=
,
∴AB=
=
=12,
∴AC=AB=12,
∵点P、M分别为BC、AB边的中点,
∴PM=
AC=6,
(2)如图2,
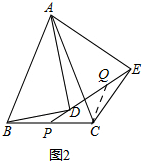
在截取ED上截取EQ=PD,
∵∠ADB=90°,
∴∠BDP+∠ADE=90°,
∵AD=AE,
∴∠ADE=∠AED,
∵把△ABD绕点A逆时针旋转一定角度,得到△ACE,
∴∠AEC=∠ADB=90°
∵∠AED+∠PEC=90°,
∴∠BDP=∠PEC,
在△BDP和△CEQ中,
,
∴△BDP和△CEQ,
∴BP=CQ,∠DBP=∠QCE,
∵∠CPE=∠BDP+∠DBP,∠PQC=∠PEC+∠QCE,
∴∠EPC=∠PQC,
∴PC=CQ,
∴BP=CP
(3)BF2+FC2=2AD2,
理由:如图3,
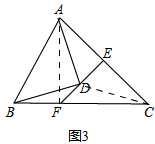
连接AF,∵EF⊥AC,且AE=EC,
∴FA=FC,∠FAC=∠FCA,
∵EF⊥AC,且AE=EC,
∴∠DAC=∠DCA,DA=DC,
∵AD=BD,
∴BD=DC,
∴∠DBC=∠DCB,
∵∠FAC=∠FCA,∠DAC=∠DCA,
∴∠DAF=∠DCB,
∴∠DAF=∠DBC,
∴∠AFB=∠ADB=90°,
在RT△ADB中,DA=DB,
∴AB2=2AD2,
在RT△ABB中,BF2+FA2=AB2=2AD2,
∵FA=FC
∴BF2+FC2=2AD2.
| 3 |
∴cos∠BAD=
| AD |
| AB |
∴AB=
| AD |
| cos∠BAD |
6
| ||
| cos30° |
∴AC=AB=12,
∵点P、M分别为BC、AB边的中点,
∴PM=
| 1 |
| 2 |
(2)如图2,

在截取ED上截取EQ=PD,
∵∠ADB=90°,
∴∠BDP+∠ADE=90°,
∵AD=AE,
∴∠ADE=∠AED,
∵把△ABD绕点A逆时针旋转一定角度,得到△ACE,
∴∠AEC=∠ADB=90°
∵∠AED+∠PEC=90°,
∴∠BDP=∠PEC,
在△BDP和△CEQ中,
|
∴△BDP和△CEQ,
∴BP=CQ,∠DBP=∠QCE,
∵∠CPE=∠BDP+∠DBP,∠PQC=∠PEC+∠QCE,
∴∠EPC=∠PQC,
∴PC=CQ,
∴BP=CP
(3)BF2+FC2=2AD2,
理由:如图3,

连接AF,∵EF⊥AC,且AE=EC,
∴FA=FC,∠FAC=∠FCA,
∵EF⊥AC,且AE=EC,
∴∠DAC=∠DCA,DA=DC,
∵AD=BD,
∴BD=DC,
∴∠DBC=∠DCB,
∵∠FAC=∠FCA,∠DAC=∠DCA,
∴∠DAF=∠DCB,
∴∠DAF=∠DBC,
∴∠AFB=∠ADB=90°,
在RT△ADB中,DA=DB,
∴AB2=2AD2,
在RT△ABB中,BF2+FA2=AB2=2AD2,
∵FA=FC
∴BF2+FC2=2AD2.
看了 在△ABC中,以AB为斜边,...的网友还看了以下:
正方体ABCD-A’B"C"D"中P,Q,R分别是AB,AD,BC的中点,那么正方体的过P,Q,R 2020-05-13 …
1、在△ABC中,∠A=π/6,D是BC边上任意一点(D与B,C不重合),且向量AB的模^2=向量 2020-05-14 …
1.已知a,b,c为△ABC的边,且满足a²(c²-a²)=b²(c²-b²),试判断此三角形的形 2020-06-05 …
在△ABC中,设a,b,c分别为∠A,∠B,∠C的对边,∠A的平分线AD交BC于D,且∠A=60度 2020-06-23 …
在△ABC中,角A,B,C的对边分别为a,b,c,且满足sinA:sinB:sinC=2:5:6. 2020-07-21 …
如图所示,AB垂直BC,DC垂直BC,垂足分别为点B,C{1}当AB=4,DC=1,BC=4时,在 2020-07-24 …
在三角形ABC中,三边的长分别为a,b,c(a>b)角BCA外角平分线交BA的延长线于点D,试求A 2020-07-24 …
逻辑化简问题AD+B'C+BD'怎么用公式法化简为A不好意思输错了AD+AB+AC’=A 2020-08-01 …
一道初三数学题ADBC(先把ADC三点连起来然后连AB)已知等腰三角形ADC,AD=AC.B是线段D 2020-12-31 …
初二菱形的判定四边形四边依次为a,b,c,d,且满足a平方+b平方+c平方+d平方-ab-bc-cd 2021-01-22 …