早教吧作业答案频道 -->数学-->
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.(1)当∠BAC满足什么条件时,四边形ADFE为矩形?(2)当∠BAC满足什么条件时,四边形ADFE不存在?(3)当△ABC
题目详情
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.
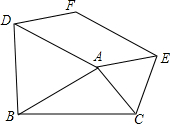
(1)当∠BAC满足什么条件时,四边形ADFE为矩形?
(2)当∠BAC满足什么条件时,四边形ADFE不存在?
(3)当△ABC满足什么条件时,四边形ADFE为菱形?
(4)当△ABC满足什么条件时,四边形ADFE为正方形?
(以上4小题,都不需说明理由)

(1)当∠BAC满足什么条件时,四边形ADFE为矩形?
(2)当∠BAC满足什么条件时,四边形ADFE不存在?
(3)当△ABC满足什么条件时,四边形ADFE为菱形?
(4)当△ABC满足什么条件时,四边形ADFE为正方形?
(以上4小题,都不需说明理由)
▼优质解答
答案和解析
∵DF∥AE,EF∥AD,
∴四边形ADFE是平行四边形,
∵△ABD与△ACE是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
(1)当∠BAC=150°时,
理由:∵∠DAE=360°-∠BAC-∠DAB-∠EAC=90°,
∴∠BAC=150°,四边形ADFE为矩形.
(2)当∠BAC=60°时,平行四边形ADFE不存在.
理由:∵∠DAE=∠DAB+∠BAC+∠EAC=60°+60°+60°=180°,
∴D,A,E共线,
∴平行四边形ADFE不存在.
(3)当AB=AC时,平行四边形ADFE是菱形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
(3)AB=AC时,且∠BAC=150°,四边形ADFE为正方形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
∵∠BAC=150°,
∴∠DAE=90°,
∴四边形ADFE为正方形.
∴四边形ADFE是平行四边形,
∵△ABD与△ACE是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
(1)当∠BAC=150°时,
理由:∵∠DAE=360°-∠BAC-∠DAB-∠EAC=90°,
∴∠BAC=150°,四边形ADFE为矩形.
(2)当∠BAC=60°时,平行四边形ADFE不存在.
理由:∵∠DAE=∠DAB+∠BAC+∠EAC=60°+60°+60°=180°,
∴D,A,E共线,
∴平行四边形ADFE不存在.
(3)当AB=AC时,平行四边形ADFE是菱形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
(3)AB=AC时,且∠BAC=150°,四边形ADFE为正方形.
理由:∵AD=AB,AE=AC,AB=AC,
∴AD=AE,
∵四边形ADFE是平行四边形,
∴平行四边形ADFE是菱形.
∵∠BAC=150°,
∴∠DAE=90°,
∴四边形ADFE为正方形.
看了 如图,分别以△ABC的边AB...的网友还看了以下:
E是平行四边形ABCD对角线交点,过点A,B,C,D,E分别向直线l引垂线,垂足分别为E是平行四边形 2020-03-31 …
四边形cedf的面积会不会随三角尺的转动而发生变化在Rt△ABC中,∠C=90°,AC=BC=4, 2020-04-13 …
矩形ABCD的对角线相交于0点DE//AC,AE//BD,DE,AE交于点E,四边形DOAE是什么 2020-04-25 …
在平行四边形ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动在平行四边形AB 2020-05-13 …
已知矩形ABCD的周长80cm,AE平分角BAD,交BC于点E,四边形AECD的周长比三角形ABE 2020-05-16 …
如图,平行四边形ABCD中,AE=CG,DH=BF,连结E,F,G,H,E,则四边形EFHG是?如 2020-05-16 …
如图,四边形ABCD是平行四边形,点E、F分别为AD、BC边上的点,且AE=CF求证:四边形BED 2020-05-16 …
如图1,在平行四边形ABCD中,AB=2AD,E,F分别为AB,CD的中点,沿EF将四边形AEFD 2020-05-17 …
(2013•镇江二模)如图1,在四边形ABCD的AB边上任取一点E(点E不与点A、点B重合),分别连 2020-11-12 …
阅读理如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把 2020-12-25 …