早教吧作业答案频道 -->数学-->
阅读理如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,若这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相
题目详情
阅读理 如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,若这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题.
(1)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(2)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
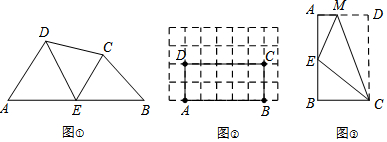
(1)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(2)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.

▼优质解答
答案和解析
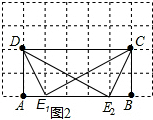
(2)如图所示:点E是四边形ABCD的边AB上的强相似点,
(3)结论:BC=
AB.
理由:如图③中,
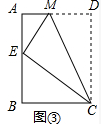
∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=
∠BCD=30°,
BE=
CE=
AB.
∴点E是AB的中点时,点E恰好是四边形ABCM的边AB上的一个强相似点,
设AE=BE=a,则EC=2a,
在Rt△EBC中,BC=
=
a,
∴AB:BC=2a:
a=2:
,
∴BC=
AB.

(3)结论:BC=
| ||
| 2 |
理由:如图③中,

∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=
| 1 |
| 3 |
BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴点E是AB的中点时,点E恰好是四边形ABCM的边AB上的一个强相似点,
设AE=BE=a,则EC=2a,
在Rt△EBC中,BC=
| EC2-EB2 |
| 3 |
∴AB:BC=2a:
| 3 |
| 3 |
∴BC=
| ||
| 2 |
看了阅读理如图①,在四边形ABCD...的网友还看了以下:
一台VCD定价560元,如果打9折出售仍获利百分之20,进价多少元?做一件衣服用了1.3米布,比计 2020-04-07 …
亲们有谁做过美容受损细胞基因重组术的吗?做这个会不会有什么不好,做这个有没有效果,有经验的不防说说 2020-04-27 …
1.小明参加了一个哑谜竞猜会,只见桌上放着五个无花果,要求猜谜人做两个动作,表示两个成语.小明拿起 2020-05-17 …
正多边形和圆的定义把一个正多边形的叫做这个正多边形的中心.叫做这个正多边形的半径.叫做正多边形的中 2020-06-16 …
1、琳琳做了一个圆柱形的灯笼,直径是20厘米,高是30厘米,上下底面的中间分别留出了78.5平方的 2020-06-21 …
节假日三薪的计算方式,所谓的三倍算底薪的一倍吗?底薪是800,节假日的三薪这样算对吗?(800/3 2020-07-05 …
没有盖的圆柱形铁皮水桶,高是12分米,底面直径是高的四分之三.做这个水桶大约用铁皮多少平方分米 2020-07-07 …
范增数目项王举所佩玉块以示之者三的“三”做什么成分是不是状语 2020-07-10 …
(2)不仅是酒,母亲终年的,做这做那,做出新鲜别致的东西总是要分给别人吃。A.勤勤恳恳B.勤勤快快 2020-07-15 …
由数与字母的组成的代数式叫做单项式.单独一个数或一个字母也是单项式.单项式中的叫做这个单项式的系数 2020-07-31 …