早教吧作业答案频道 -->数学-->
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是()A、60°B、72°C、66°D、不确定
题目详情
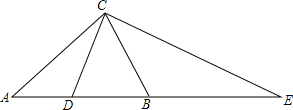 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
▼优质解答
答案和解析
考点:
等腰三角形的性质
专题:
分析:
取AC的中点F,连接BF,根据等腰三角形的轴对称性可得∠DCB=∠FBC,再判断出BF是△ACE的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得BF∥CE,根据两直线平行,内错角相等可得∠BCE=∠FBC,然后根据∠DCE=∠BCE+∠DCB计算即可得解.
如图,取AC的中点F,连接BF,∵AC=AB,CD是中线,∴∠DCB=∠FBC=36°,∵BE=AB,∴BF是△ACE的中位线,∴BF∥CE,∴∠BCE=∠FBC=36°,∴∠DCE=∠BCE+∠DCB=36°+36°=72°.故选B.
点评:
本题考查了等腰三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于作辅助线构造出三角形的中位线.
考点:
等腰三角形的性质
专题:
分析:
取AC的中点F,连接BF,根据等腰三角形的轴对称性可得∠DCB=∠FBC,再判断出BF是△ACE的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得BF∥CE,根据两直线平行,内错角相等可得∠BCE=∠FBC,然后根据∠DCE=∠BCE+∠DCB计算即可得解.
如图,取AC的中点F,连接BF,∵AC=AB,CD是中线,∴∠DCB=∠FBC=36°,∵BE=AB,∴BF是△ACE的中位线,∴BF∥CE,∴∠BCE=∠FBC=36°,∴∠DCE=∠BCE+∠DCB=36°+36°=72°.故选B.
点评:
本题考查了等腰三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于作辅助线构造出三角形的中位线.
看了 锐角△ABC中,AC=AB,...的网友还看了以下:
求一数列.高2.a(n+1)=2an/2an+1已知a1=1a(n+1)=2an/2an+1求数列 2020-04-25 …
怎样使用matlab解下面的代数方程?急.syms a b c d e;2*b^2=a^2+c^2 2020-05-16 …
高数二多元函数问题由z=f(x,y)可解出y=y(z,x),将z=f(x,y)对x求偏导,得0=d 2020-06-18 …
其中OP为操作数、R为通用寄存器地址、试说明在下列情况下能访问的最大主存区为多少个机器字?1)D为 2020-06-24 …
100的素因数有()A.1个B.2个C.3个D.4个100以内同时具有只含有素因数2、3、5的合数 2020-06-25 …
1.设abcd是四个整数,且使m=(ab+cd)^2-1/4(a^2+b^2-c^2-d^2)^2 2020-07-09 …
二阶导数的表达式分母为什么是dx^2?d/dx(dy/dx)为什么不等于d^2•y/(dx)^2= 2020-08-02 …
若a、b互为倒数,c、d互为相反数|m|=2,(c+d)*a/b+3ab-m²=-2³-|-3|=, 2020-11-20 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
函数f(x)的定义域为D,若满足如下两条件:①f(x)在D内是单调函数;②存在[m/2,n/2]是D 2021-01-04 …