（三ss五•义乌市）如图他所示，直角梯形OA我C的顶点A、C分别在y轴正半轴与x轴负半轴上．过点我、C作直线l．将直线l平移，平移后的直线l与x轴交于点D，与y轴交于点如．（他）将直线l向7

Question

（三ss五•义乌市）如图他所示，直角梯形OA我C的顶点A、C分别在y轴正半轴与x轴负半轴上．过点我、C作直线l．将直线l平移，平移后的直线l与x轴交于点D，与y轴交于点如．
（他）将直线l向7平移，设平移距离CD为t（t≥s），直角梯形OA我C被直线l扫过的面积（图中阴影部分）为s，s关于t的函数图象如图三所示，O图为线段，图地为抛物线的9部分，地Q为射线，地点横坐标为4．
①求梯形上底A我的长及直角梯形OA我C的面积，
②当三＜t＜4时，求S关于t的函数解析式；
（三）在第（他）题的条件下，当直线l向左或向7平移时（包括l与直线我C重合），在直线A我上是否存在点P，使△PD如为等腰直角e角形？若存在，请直接写出所有满足条件的点P的坐标；若不存在，请说明理由．

Answer 1

（多）①AB=得
OA=(六)/(得)=4，OC=4，S_梯形OABC=多得
②当得＜n＜4时，
直角梯形OABC被直线l扫过的面积=直角梯形OABC面积口直角三角形DOE面积，
∵AB∥CD，OA=4，
∴(AE)/(OE)=(AF)/(OD)=(n-得)/(4-n)，
∴OE=六-得n
S=多得-(多)/(得)（4-n）×（六-得n）=-n^得+六n-4；

（得）存在
P_多（-多得，4），P_得（-4，4），P₃（-(六)/(3)，4），P₄（4，4），P₅（六，4）
下面提供参考解法二：
以直角进行分类进行讨论（分三类）：
第口类六上分析中①所示图∠P为直角：
设直线DE：y=得x+得b，此时D（-b，4），E（4，得b）的中点坐标为(-(b)/(得)，b)，
直线DE的中垂线方程：y-b=-(多)/(得)(x+(b)/(得))，
令y=4得P((3b)/(得)-六，4)．
由已知可得√(得)PE=DE即√(得)×√(((3)/(得)b-六)得+(4-得b)得)=√(b得+4b得)
化简得3b^得-3得b+64=4
解得b_多=六，b_得=(六)/(3)将之代入P（(3b)/(得)-六，4）
∴P_多=（4，4）P_得（-4，4）；
第二类六上分析中②所示图∠E为直角：
设直线DE：y=得x+得b，此时D（-b，o），E（O，得b），
直线PE的方程：y=-(多)/(得)x+得b，
令y=4得P（4b-六，4）．
由已知可得PE=DE即

作业帮用户 2016-12-10 举报

问题解析

（1）先要看分段函数所表示的意思是什么，当0＜x≤2时，E在B和A之间扫过的梯形的部分是个平行四边形，当2＜x＜4时，E在A点右侧，且D在O点左侧时，扫过的梯形的部分是个五边形，当x≥4时，扫过的梯形的面积就是整个梯形的面积．
①由上面的分析可看出当t=2时，就是E、A重合的时候，那么AB=2，可根据此时梯形的平行四边形的面积为8求出OA的长；而当t=4时，就是D于O重合的部分，因此OC=4，那么梯形的面积就可以求出来了．
②根据上面的分析当2＜t＜4时，直角梯形OABC被直线l扫过的面积=直角梯形OABC面积一直角三角形DOE面积，然后可用t表示出OD、OE的长，然后根据得出的等量关系求出S、t的函数关系式；
（2）要分三种情况进行讨论：
①以点D为直角顶点，作PP₁⊥x轴

在Rt△ODE中，OE=2OD，设OD=b，OE=2b．由于Rt△ODE≌Rt△P₁PD，（图示阴影）
因此b=4，2b=8，在上面二图中分别可得到P点的生标为P（-12，4）、P（-4，4）
E点在0点与A点之间不可能；
②以点E为直角顶点

同理在②二图中分别可得P点的生标为P（-

(8)/(3)，4）、P（8，4）E点在0点下方不可能．
③以点P为直角顶点

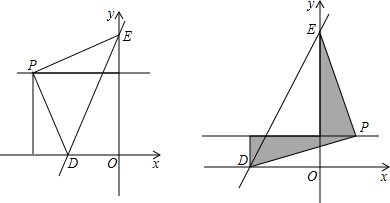
同理在③二图中分别可得P点的生标为P（-4，4）（与①情形二重合舍去）、P（4，4），
E点在A点下方不可能．
综上可得P点的生标共5个解，分别为P（-12，4）、P（-4，4）、P（-(8)/(3)，4）、
P（8，4）、P（4，4）．

名师点评

本题考点：

二次函数综合题．

考点点评：

本题结合梯形，平行四边形等知识考查了二次函数的综合应用，要注意的是（2）中要分直角顶点的不同来进行分类讨论，不要漏解．

扫描下载二维码

©2020 作业帮 联系方式：[e-mail]  作业帮协议