早教吧作业答案频道 -->数学-->
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.(1)求证:平面CFG⊥平面ACE;(2)在AC上是否一点H,使得EH∥平面CFG?若存在,求出CH的
题目详情
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.
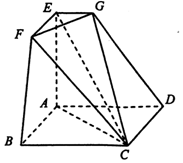
(1)求证:平面CFG⊥平面ACE;
(2)在AC上是否一点H,使得EH∥平面CFG?若存在,求出CH的长;若不存在,请说明理由.

(1)求证:平面CFG⊥平面ACE;
(2)在AC上是否一点H,使得EH∥平面CFG?若存在,求出CH的长;若不存在,请说明理由.
▼优质解答
答案和解析
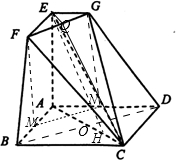 (1)证明:连接BD交AC于点O,则BD⊥AC,
(1)证明:连接BD交AC于点O,则BD⊥AC,
设AB,AD的中点分别为M,N,连接MN,则MN∥BD,
连接FM,GN,则FM∥GN且FM=GN,所以MN∥FG,所以BD∥FG
由于AE⊥平面ABCD,所以 AE⊥BD,
所以FG⊥AC,FG⊥AE,所以FG⊥平面ACE,FG⊂平面CFG,
所以平面CFG⊥平面ACE.
(2)设平面ACE交FG于Q,则Q为FG的中点,
连接EQ,CQ,取CO的中点为H,则CH∥EQ,CH=EQ=
,
所以四边形EQCH为平行四边形,
所以EH∥CQ,EH⊄平面CFQ,CQ⊂平面CFQ,
所以EH∥平面CFG,
所以,在AC上存在一点H,使得EH∥平面CFG,且CH=
.
 (1)证明:连接BD交AC于点O,则BD⊥AC,
(1)证明:连接BD交AC于点O,则BD⊥AC,设AB,AD的中点分别为M,N,连接MN,则MN∥BD,
连接FM,GN,则FM∥GN且FM=GN,所以MN∥FG,所以BD∥FG
由于AE⊥平面ABCD,所以 AE⊥BD,
所以FG⊥AC,FG⊥AE,所以FG⊥平面ACE,FG⊂平面CFG,
所以平面CFG⊥平面ACE.
(2)设平面ACE交FG于Q,则Q为FG的中点,
连接EQ,CQ,取CO的中点为H,则CH∥EQ,CH=EQ=
| ||
| 2 |
所以四边形EQCH为平行四边形,
所以EH∥CQ,EH⊄平面CFQ,CQ⊂平面CFQ,
所以EH∥平面CFG,
所以,在AC上存在一点H,使得EH∥平面CFG,且CH=
| ||
| 2 |
看了 如图所示的空间几何体ABCD...的网友还看了以下:
最好有图片,不要直接答案如图12-11,在梯形ABCD中,AD∥BC,∠C=90°,AD=b,BC= 2020-03-30 …
一道数学选择 帮下忙A(a+b)(a分之1+b分之一)大于等于四 B a的三次方+b的三次方大于等 2020-05-16 …
如果两个相似三角形对应高的比为5比4,对应中线的比为?对应叫平分线的比?若三角形ABC与三角形A' 2020-06-02 …
在长方形abcd中AB=a,AD=b,E是AD边上一点,AE:AD=n1·当n=----时,S△d 2020-06-08 …
在长方形abcd中AB=a,AD=b,E是AD边上一点,AE:AD=n1·当n=----时,S△d 2020-06-08 …
如图,在三角形ABC中,点D.E在边BC上,角CAE=角B,E是CD的中点,且AD平分角BAE.1 2020-06-08 …
帮个忙解三条数学问题!1.a,b,c是2x^3+x^2-4x+1=0的根,求:(1)a^2+b^2 2020-06-24 …
化学有毒气体A.D是两种常见的固体,其中D为亮红色;B.E是两种常见的气体,其中气体E有剧毒,他们 2020-07-11 …
泰历中年份前面的B.E.是什么意思?比如:21JuneB.E.2552 2020-07-23 …
若函数f(x)在其定义域内某一区间[a,b]e连续,且对[a,b]中任意实数x地,x2,都有f(x 2020-07-29 …