早教吧作业答案频道 -->数学-->
如图,△ABC是等腰直角三角形,AB=42,D为斜边BC上的一点(D与B、C均不重合),连结AD,把△ABD绕点A按逆时针旋转后得到△ACE,连结DE,设BD=x.(1)求证:∠DCE=90°;(2)当△DCE的面积为6
题目详情
如图,△ABC是等腰直角三角形,AB=4
,D为斜边BC上的一点(D与B、C均不重合),连结AD,把△ABD绕点A按逆时针旋转后得到△ACE,连结DE,设BD=x.
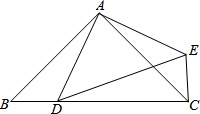
(1)求证:∠DCE=90°;
(2)当△DCE的面积为6时,求x的值;
(3)当D在斜边BC上运动时(D与B、C均不重合)四边形ADCE的面积S是否随着x的变化而变化?若变化,请求出S与x之间的函数关系式;若不变,求出S的值.
| 2 |

(1)求证:∠DCE=90°;
(2)当△DCE的面积为6时,求x的值;
(3)当D在斜边BC上运动时(D与B、C均不重合)四边形ADCE的面积S是否随着x的变化而变化?若变化,请求出S与x之间的函数关系式;若不变,求出S的值.
▼优质解答
答案和解析
(1)∵△ABD绕点A按逆时针旋转后得到△ACE,
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,
∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB=4
,
∴BC2=AC2+AB2=(4
)2+(4
)2=64,
∴BC=8,
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=8,
∴DC=8-x,
∴Rt△DCE的面积为:
DC•CE=
(8-x)x.
∴
(8-x)x=6,
即-x2+8x-12=0.
解得x=2或x=6;
(3)因为△ACE≌△ABD,
所以△ABD的面积等于△ACE的面积,
所以四边形ADCE的面积S不变,
S=
×4
×4
=16.
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,
∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB=4
| 2 |
∴BC2=AC2+AB2=(4
| 2 |
| 2 |
∴BC=8,
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=8,
∴DC=8-x,
∴Rt△DCE的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
即-x2+8x-12=0.
解得x=2或x=6;
(3)因为△ACE≌△ABD,
所以△ABD的面积等于△ACE的面积,
所以四边形ADCE的面积S不变,
S=
| 1 |
| 2 |
| 2 |
| 2 |
看了 如图,△ABC是等腰直角三角...的网友还看了以下:
△ABC,△CEF都为等腰直角三角形,当E,F在AC,BC上,∠ACB=90°,连BE,AF,M为 2020-04-11 …
(2014•自贡)阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分 2020-06-13 …
一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正 2020-06-27 …
如图,⊙o以等腰三角形abc一腰ab为直径,它交另一腰ac于e,交bc于d 求证:bc=2de 2020-06-27 …
关于等腰三角形的趣味题一个等腰三角形,把它平均分成2份后这两份还各是等腰三角形,问这样的三角形有几 2020-07-13 …
如何把三角形分成两个等腰三角形把一个三角形分成两个等腰三角形,被分的三角形不是直角、等边、等腰三角 2020-07-26 …
有一个底角为60°腰长为15cm下底长是上底长2倍的等腰梯形,把2腰分成30份,然后把对应等分点连 2020-08-02 …
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DP 2020-11-04 …
阅读理如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把 2020-12-25 …
三角形ABC为等腰三角形,点E在底边AB上有A点向B点移动(不包括A,B两点)D,F分别在腰AC,B 2020-12-25 …