早教吧作业答案频道 -->数学-->
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE
题目详情
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.
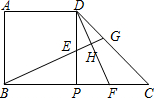
(1)求证:①△BPE≌△DPF.②BG⊥DF.
(2)试问:是否存在这样x的值,使得DF和EG互相垂直平分,若存在,请求出x的值;若不存在,请说明理由.
(3)若连结AH,在运动过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请猜想∠AHB的度数,不用说明理由.

(1)求证:①△BPE≌△DPF.②BG⊥DF.
(2)试问:是否存在这样x的值,使得DF和EG互相垂直平分,若存在,请求出x的值;若不存在,请说明理由.
(3)若连结AH,在运动过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请猜想∠AHB的度数,不用说明理由.
▼优质解答
答案和解析
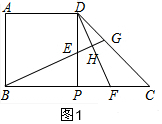 (1)①证明:如图1,
(1)①证明:如图1,
∵四边形ABPD是正方形,△DPC是等腰直角三角形,
∴BP=PD=PC,∠BPE=∠DPF=90°,
又∵DE=CF,
∴PE=PF,
∴△BPE≌△DPF;
②∵△BPE≌△DPF,
∴∠EBP=∠FDP,
又∵∠FDP+∠BFH=90°,
∴∠EBP+∠BFH=90°,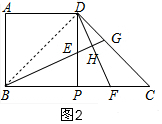
∴BG⊥DF;
(2)存在,如图2,
连结BD,若直线BG垂直平分线段DF,
则BF=BD,
∵四边形ABCD是正方形,且AB=1,
∴BD=
,
∴BF=BD=
,
∴x=CF=2-
,
此时,∠FBH=∠DBG=
×45°=22.5°,
∴∠PBH=∠PDF=22.5°,
∵∠PDC=45°,
∴∠PDF=∠CDF=22.5°,
又∵BG⊥DF,
∴EH=GH,
∴直线DF垂直平分线段EG,
∴当x=2-
时,DF和EG互相垂直平分;
(3)∠AHB的大小不改变,∠AHB=45°,理由是:
如图2,∵四边形ABCD是正方形,
∴∠BAD=90°,∠ADB=45°,
∵BG⊥DF,
∴∠DHB=90°,
∴∠BAD+∠DHB=180°,
∴A、B、H、D四点共圆,
∴∠AHB=∠ADB=45°.
 (1)①证明:如图1,
(1)①证明:如图1,∵四边形ABPD是正方形,△DPC是等腰直角三角形,
∴BP=PD=PC,∠BPE=∠DPF=90°,
又∵DE=CF,
∴PE=PF,
∴△BPE≌△DPF;
②∵△BPE≌△DPF,
∴∠EBP=∠FDP,
又∵∠FDP+∠BFH=90°,
∴∠EBP+∠BFH=90°,

∴BG⊥DF;
(2)存在,如图2,
连结BD,若直线BG垂直平分线段DF,
则BF=BD,
∵四边形ABCD是正方形,且AB=1,
∴BD=
| 2 |
∴BF=BD=
| 2 |
∴x=CF=2-
| 2 |
此时,∠FBH=∠DBG=
| 1 |
| 2 |
∴∠PBH=∠PDF=22.5°,
∵∠PDC=45°,
∴∠PDF=∠CDF=22.5°,
又∵BG⊥DF,
∴EH=GH,
∴直线DF垂直平分线段EG,
∴当x=2-
| 2 |
(3)∠AHB的大小不改变,∠AHB=45°,理由是:
如图2,∵四边形ABCD是正方形,
∴∠BAD=90°,∠ADB=45°,
∵BG⊥DF,
∴∠DHB=90°,
∴∠BAD+∠DHB=180°,
∴A、B、H、D四点共圆,
∴∠AHB=∠ADB=45°.
看了ABPD是一个边长为1的正方形...的网友还看了以下:
已知阿尔法是锐角,那2阿尔法是?A.第一象限角B.第二象限角C.小于180°的正角D.不小于直角的 2020-05-16 …
下列叙述不正确的是(数学)A.三角形的角平分线、中线、高线都是线段B.角平分线是一条射线C.三角形 2020-05-20 …
已解决已知a是锐角,那么2a是()角A.第一象限B.第二象限C.小于180度的正角D.第一或第二象 2020-07-18 …
已知θ是锐角,那么2θ是()A.第一象限角B.第二象限角C.小于180°的正角D.第一或第二象限角 2020-07-30 …
1、下列说法中正确的是()A、两点之间的所有连线中,线段最短B、射线就是直线C、两条射线组成的图形 2020-07-30 …
对于诱导公式中的角,下列说法正确的是()A.一定是锐角B.0≤<2πC.一定是正角D.是使公式有意 2020-08-02 …
第一题:已知a是锐角,那么2a是()A第一象限角B第二象限角C小于180度的正角D不大于直角的正角 2020-08-03 …
如图,直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动,直角顶点C与原点O在直线AB的两侧,则 2020-12-05 …
数学初一上册第六章评价测试卷(苏教版)6、下列语句中正确的是()A.线段AB和线段BA表示不同的线段 2021-01-08 …
所有与角α终边相同的角可表示为k*360+α+α(k属于Z),其中α的范围是什么A、一定是小于90° 2021-02-04 …