早教吧作业答案频道 -->数学-->
已知△ABC是直角三角形,∠ABC=90°,在△ABC外作直角三角形ACE,∠ACE=90°(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD
题目详情
已知△ABC是直角三角形,∠ABC=90°,在△ABC外作直角三角形ACE,∠ACE=90°
(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;
(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD,∠EAC=45°,AE=
,求四边形ABDE的面积.
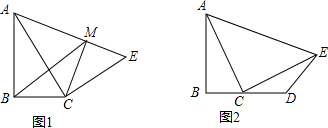
(1)如图1,过点C作CM⊥AE,垂足为M,连结BM,若AB=AM,求证:BM∥CE;
(2)如图2,延长BC至D,使得CD=BC,连结DE,若AB=BD,∠EAC=45°,AE=
| 10 |

▼优质解答
答案和解析
(1)证明:如图1中,
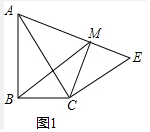
∵CM⊥AE,
∴∠ABC=∠AMC=90°,
在Rt△ACB和Rt△ACM中,
,
∴Rt△ACB≌Rt△ACM,
∴BC=CM,∵AB=AM,
∴BM⊥AC,
∵∠ACE=90°,
∴AC⊥CE,
∴BM∥CE.
(2) 如图2中,作EF⊥BD于F.
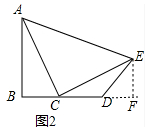
∵∠ACE=90°,∠EAC=45°,
∴∠CAE=∠CEA=45°,
∴CA=CE,∵AE=
,
∴AC=CE=
,
在Rt△ABC中,∵AB=2BC,
∴BC2+4BC2=5,
∴BC=1,AB=2,
∴CB=CD=1,
∵∠ACB+∠BAC=90°,∠ACB+∠ECF=90°,
∴∠BAC=∠ECF,
在△ABC和△CFE中,
,
∴△ABC≌△CFE,
∴BC=EF=1,
∴S四边形ABDE=S△ABC+S△ACE+S△CDE=
×1×2+
×
×
+
×1×1=4.

∵CM⊥AE,
∴∠ABC=∠AMC=90°,
在Rt△ACB和Rt△ACM中,
|
∴Rt△ACB≌Rt△ACM,
∴BC=CM,∵AB=AM,
∴BM⊥AC,
∵∠ACE=90°,
∴AC⊥CE,
∴BM∥CE.
(2) 如图2中,作EF⊥BD于F.

∵∠ACE=90°,∠EAC=45°,
∴∠CAE=∠CEA=45°,
∴CA=CE,∵AE=
| 10 |
∴AC=CE=
| 5 |
在Rt△ABC中,∵AB=2BC,
∴BC2+4BC2=5,
∴BC=1,AB=2,
∴CB=CD=1,
∵∠ACB+∠BAC=90°,∠ACB+∠ECF=90°,
∴∠BAC=∠ECF,
在△ABC和△CFE中,
|
∴△ABC≌△CFE,
∴BC=EF=1,
∴S四边形ABDE=S△ABC+S△ACE+S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
看了 已知△ABC是直角三角形,∠...的网友还看了以下:
甲乙两人在400米的环形跑道上练习跑步,若同向跑,甲a分钟可超乙一圈;若反向跑,两人每隔b分钟相遇 2020-04-27 …
1.直三棱柱ABC--A'B'C'中,各侧棱和底面的边长均为a,点D是侧棱CC'上任意一点,连接A 2020-06-27 …
已知直二面角a-l-b,点A属于面a,且AC垂直于l已知直二面角a-l-b,点A属于面a,AC垂直 2020-06-27 …
NH3通过铁触媒会有什么现象?a升NH3通过灼热的装有铁触媒的硬质玻璃管,气体体积变为b升(气体体 2020-07-03 …
已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b且AB=2,CD=1,则a与b所成 2020-07-09 …
4b可以表示为()A.4+bB.b×b×b×bC.b+b+b+bD.b4 2020-07-09 …
如图,正方体ABCD-A'B'C'D'的棱长为a,连接A'C',A'D',BD,BC',CD',得 2020-07-22 …
已知a,b是异面直线,A,B属于a;C,D属于b,AC垂直b,BD垂直b.且AB=2.CD=1,则 2020-08-02 …
在长方体ABCD-A'B'C'D',底面是边长为2的正方形,高为4,则点A'到截面AB'D'的距离 2020-08-02 …
如图所示,用两根细线AC和BD悬挂一薄板.下列说法正确的是()A.薄板的重心一定在AC和BD的延长线 2020-11-30 …