如图，在正方形ABCD中，点P为AB上一点，AQ⊥DP交BC于点Q，以AQ为边作平行四边形ABHQ，过点C作CF⊥DP于点F，点O为正方形对角线的交点，连OF，则下列结论：①BH=DP；②EF=2OF；③OF∥BE；④若正方

Question

如图，在正方形ABCD中，点P为AB上一点，AQ⊥DP交BC于点Q，以AQ为边作平行四边形ABHQ，过点C作CF⊥DP于点F，点O为正方形对角线的交点，连OF，则下列结论：
①BH=DP；
②EF=

√(2)OF；
③OF∥BE；
④若正方形的边长为2，则BE的最小值为√(5)-1；
其中正确的有（　　）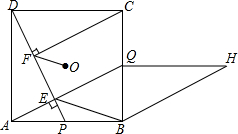

A. 4个

B. 3个

C. 2个

D. 1个

Answer 1

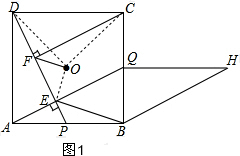①如图1，在正方形ABCD中，
∴AD=AB，∠DAB=∠ABC=90°，
∴∠DAQ+∠QAB=90°，
∵AQ⊥PD，
∴∠AED=90°，
∴∠DAQ+∠ADP=90°，
∴∠QAB=∠ADP，
∴△DAP≌△ABQ，
∴AQ=PD，
∵四边形ABHQ是平行四边形，
∴BH=AQ，
∴BH=PD；
所以此选项正确；
②如图1，连接OD、OC、OE，则OD=OC，
∵∠ADE+∠EDC=90°，∠DCF+∠EDC=90°，
∴∠ADE=∠DCF，
∵∠ADO=∠DCO=45°，
∴∠EDO=∠FCO，
∵AD=DC，∠AED=∠DFC=90°，
∴△DAE≌△CDF，
∴CF=DE，
∴△DOE≌△COF，
∴OE=OF，∠DOE=∠COF，
∴∠DOE-∠DOF=∠COF-∠DOF，
即：∠FOE=∠DOC，
∵∠DOC=90，
∴∠FOE=90°，
∴△FOE是等腰直角三角形，
∴EF=√(2)OF；
所以此选项正确；
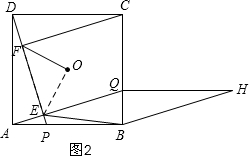
③当∠OEB=∠FOE=90°时，OF∥BE，
但∠OEB不一定等于90°，如图2，∠OEB<90°，
所以此选项不正确；
④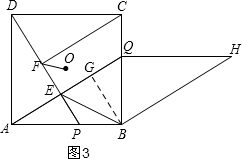如图3，当BE=BQ时，BE最小，
过B作BG⊥AQ于Q，
则△AED≌△BGA，
∴AE=BG，
∵∠EAP+∠AQB=90°，∠GBQ+∠AQB=90°，
∴∠EAP=∠GBQ，
∵∠AEP=∠BGQ=90°，
∴△AEP≌△BGQ，
∴BQ=AP，
设BE=x，BG=a，则BQ=AP=x，AE=a，
∵PE∥BG，
∴(AP)/(AB)=(EP)/(BG)，
∴(x)/(2)=(EP)/(a)，
∴EP=(ax)/(2)，
∵BE=BQ，BG⊥AQ，
∴EG=GQ=PE=(ax)/(2)，
在Rt△ABG中，BG²=QG•AG，
a2=(ax)/(2)(a+(ax)/(2))，
解得：x=-1±√(5)，
x₁=-1-√(5)（舍去），x₂=-1+√(5)，
∴BE=√(5)-1，
即若正方形的边长为2，则BE的最小值为√(5)-1；
所以此选项正确；
所以本题正确的结论有3个，故选B．