如图，O是△ABC的外接圆，已知AD平分∠BAC交O于点D，连结CD，延长AC，BD，相交于点F．现给出下列结论：①若AD=5，BD=2，则DE=25；②∠ACB=∠DCF；③△FDA∽△FCB；④若直径AG⊥BD交BD于点H，AC=FC=4

Question

如图， O是△ABC的外接圆，已知AD平分∠BAC交 O于点D，连结CD，延长AC，BD，相交于点F．现给出下列结论：
①若AD=5，BD=2，则DE=

(2)/(5)；
②∠ACB=∠DCF；
③△FDA∽△FCB；
④若直径AG⊥BD交BD于点H，AC=FC=4，DF=3，则cosF=(41)/(48)；
则正确的结论是（　　）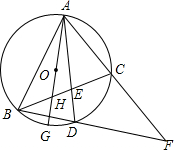

A. ①③

B. ②③④

C. ③④

D. ①②④

Answer 1

①如图1，

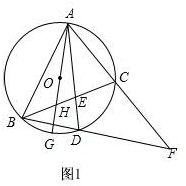
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∵∠CAD=∠CBD，
∴∠BAD=∠CBD，
∵∠BDE=∠BDE，
∴△BDE∽△ADB，
∴(BD)/(AD)=(DE)/(BD)，
由AD=5，BD=2，可求DE=(4)/(5)，
①不正确；
②如图2，

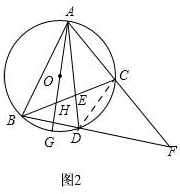
连接CD，
∠FCD+∠ACD=180°，∠ACD+∠ABD=180°，
∴∠FCD=∠ABD，
若∠ACB=∠DCF，因为∠ACB=∠ADB，
则有：∠ABD=∠ADB，与已知不符，
故②不正确；
③如图3，

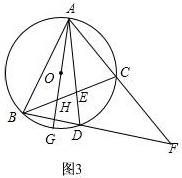
∵∠F=∠F，∠FAD=∠FBC，
∴△FDA∽△FCB；
故③正确；
④如图4，

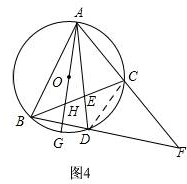
连接CD，由②知：∠FCD=∠ABD，
又∵∠F=∠F，
∴△FCD∽△FBA，
∴(FC)/(FB)=(FD)/(FA)，
由AC=FC=4，DF=3，可求：AF=8，FB=(32)/(3)，
∴BD=BF-DF=(23)/(3)，
∵直径AG⊥BD，
∴DH=(23)/(6)，
∴FG=(41)/(6)，
∴cosF=(FG)/(AF)=(41)/(48)，
故④正确；
故选：C．