早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.(1)求证:△ADE∽△ACD;(2)若△DCE为直角三角形,求线段BD的长;(3)求线段CE长的取值范
题目详情
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.
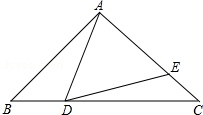
(1)求证:△ADE∽△ACD;
(2)若△DCE为直角三角形,求线段BD的长;
(3)求线段CE长的取值范围.(直接写出答案)

(1)求证:△ADE∽△ACD;
(2)若△DCE为直角三角形,求线段BD的长;
(3)求线段CE长的取值范围.(直接写出答案)
▼优质解答
答案和解析
(1)证明:∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠DAE=∠CAD,
∴△ADE∽△ACD;
(2)△DCE为直角三角形,有以下两种可能:①∠CED=90°②∠EDC=90°.
①当∠CED=90°时,即∠AED=90°,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.
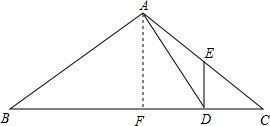 ②当∠EDC=90°时,
②当∠EDC=90°时,
∵∠ADE+∠EDC=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠EDC=90°,
如图,过A作AF⊥BC于F,则BF=8,
∵∠B是公共角,∠AFB=∠BAD=90°,
∴△BFA∽△BAD,
∴
=
,
∴
=
,
∴BD=
.
综上所述,△DCE为直角三角形时,BD=8或BD=
.
(3)由(2)得:∠EDC=∠BAD,
∵∠B=∠C,
∴△CDE∽△BAD,
设BD=y,CE=x,
∴
=
,
∴
=
,
整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,
∵0<BD<16,
∴0<x≤6.4.
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠DAE=∠CAD,
∴△ADE∽△ACD;
(2)△DCE为直角三角形,有以下两种可能:①∠CED=90°②∠EDC=90°.
①当∠CED=90°时,即∠AED=90°,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.
 ②当∠EDC=90°时,
②当∠EDC=90°时,∵∠ADE+∠EDC=∠B+∠BAD,∠ADE=∠B,
∴∠BAD=∠EDC=90°,
如图,过A作AF⊥BC于F,则BF=8,
∵∠B是公共角,∠AFB=∠BAD=90°,
∴△BFA∽△BAD,
∴
| AB |
| BD |
| BF |
| AB |
∴
| 10 |
| BD |
| 8 |
| 10 |
∴BD=
| 25 |
| 2 |
综上所述,△DCE为直角三角形时,BD=8或BD=
| 25 |
| 2 |
(3)由(2)得:∠EDC=∠BAD,
∵∠B=∠C,
∴△CDE∽△BAD,
设BD=y,CE=x,
∴
| AB |
| DC |
| BD |
| CE |
∴
| 10 |
| 16-y |
| y |
| x |
整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,
∵0<BD<16,
∴0<x≤6.4.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
三角形已知平行四边形abcd,ab边上一点e,bc上一点f,三角形ade的面积5,三角形bef面已 2020-05-17 …
在三角形ABC中,角BAC=90度,AB=AC,角ABC的平分线交AC于点D,过点C作BD垂线交B 2020-05-19 …
仙人掌上面长出一根长条形状的东西是什么?我以前买的一个三面(三个角)的那种仙人掌上面有个黄色的花( 2020-07-06 …
已知三角形ABC,D是BC延长线上的点,F是AB延长线上的点,角ACD的平分线叫BA的延长线于E, 2020-07-11 …
数学题目,高手新手都可以进!已知等腰直角三角形ABC,B为直角,直角边长为1,在AB,AC上分别取 2020-08-02 …
在三角形ABC中,角A角B的平分线分别交对边于D,E角C的外角平分线交对边延长线于F,求证:D、E 2020-08-03 …
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DP 2020-11-04 …
在等边三角形ABC中,D是BC边上一点,三角形DEB为等边三角形,CE的延长线与AB的延长线交于M, 2021-01-02 …
内眼角上长了疙瘩 2021-04-16 …
嘴角上长泡怎么办 2021-04-19 …