早教吧作业答案频道 -->数学-->
在等腰Rt△ABC和等腰Rt△A1B1C1中,斜边B1C1中点O也是BC的中点.(1)如图1,则AA1与CC1的数量关系是;位置关系是.(2)如图2,将△A1B1C1绕点O顺时针旋转一定角度,上述结论是否仍然成
题目详情
在等腰Rt△ABC和等腰Rt△A1B1C1中,斜边B1C1中点O也是BC的中点.
(1)如图1,则AA1与CC1的数量关系是___;位置关系是___.
(2)如图2,将△A1B1C1绕点O 顺时针旋转一定角度,上述结论是否仍然成立,请证明你的结论.
(3)如图3,在(2)的基础上,直线AA1、CC1交于点P,设AB=4,则PB长的最小值是___.
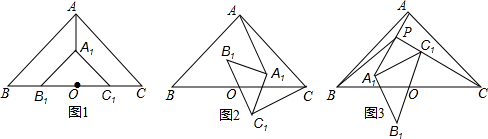
(1)如图1,则AA1与CC1的数量关系是___;位置关系是___.
(2)如图2,将△A1B1C1绕点O 顺时针旋转一定角度,上述结论是否仍然成立,请证明你的结论.
(3)如图3,在(2)的基础上,直线AA1、CC1交于点P,设AB=4,则PB长的最小值是___.

▼优质解答
答案和解析
(1)连接AO,A1O,如图1,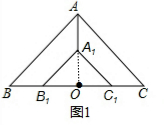
∵△ABC和△A1B1C1都是等腰直角三角形,斜边B1C1中点O也是BC的中点,
∴AO⊥OC,AO=OC,A1O⊥OC1,OA1=OC1,
∴A点、A1点、O点共线,
∴AA1⊥C1C,OA-OA1=OC-OC1,
∴AA1=C1C;
(2)上述结论仍然成立.理由如下: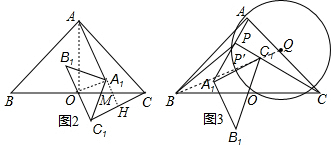
连接OA,A1O,如图2,
∵△A1B1C1绕点O 顺时针旋转一定角度,
∴∠AOA1=∠COC1,
在△OAA1和△OCC1中,
,
∴△OAA1≌△OCC1,
∴AA1=C1C,∠OAA1=∠OCC1,
延长AA1交CC1于H,交BC于M,如图2,
∵∠AMO=∠CMH,
∴∠MHC=∠MOA=90°,
∴AA1⊥C1C.
(3)∵AA1⊥C1C,
∴∠APC=90°,
∴点P在以AC为直径的圆上,
以AC为直角作 Q,连接BQ交 Q于P′,如图3,此时BP′最小,
在Rt△ABQ中,BQ=
=
=2
,
∴BP′=BQ-QP′=2
-2,
∴PB长的最小值是2
-2.
故答案为:相等、垂直;2
-2.

∵△ABC和△A1B1C1都是等腰直角三角形,斜边B1C1中点O也是BC的中点,
∴AO⊥OC,AO=OC,A1O⊥OC1,OA1=OC1,
∴A点、A1点、O点共线,
∴AA1⊥C1C,OA-OA1=OC-OC1,
∴AA1=C1C;
(2)上述结论仍然成立.理由如下:

连接OA,A1O,如图2,
∵△A1B1C1绕点O 顺时针旋转一定角度,
∴∠AOA1=∠COC1,
在△OAA1和△OCC1中,
|
∴△OAA1≌△OCC1,
∴AA1=C1C,∠OAA1=∠OCC1,
延长AA1交CC1于H,交BC于M,如图2,
∵∠AMO=∠CMH,
∴∠MHC=∠MOA=90°,
∴AA1⊥C1C.
(3)∵AA1⊥C1C,
∴∠APC=90°,
∴点P在以AC为直径的圆上,
以AC为直角作 Q,连接BQ交 Q于P′,如图3,此时BP′最小,
在Rt△ABQ中,BQ=
| AB2+AQ2 |
| 42+22 |
| 5 |
∴BP′=BQ-QP′=2
| 5 |
∴PB长的最小值是2
| 5 |
故答案为:相等、垂直;2
| 5 |
看了 在等腰Rt△ABC和等腰Rt...的网友还看了以下:
1,一次函数Y=kx+b,与x轴的交点坐标是什么?2.已知p=(E/R+r)^2*R,其中E与r是 2020-05-13 …
等比数列{an}的前项和为Sn,已知对任意的n∈N*,点(n,Sn)均在函数y=b的x次方+r(b 2020-05-13 …
一道数列题等比数列{an}的前n项和为Sn,已知对任意的n(n属于自然数),点(n,Sn)均在函数 2020-05-13 …
等比数列{an}的前n项和为Sn,已知对任意的n属于N*.点(n,Sn)均在函数y=b^x+r(b 2020-05-13 …
在matlab中如何筛选得出的结果,我只需要多个结果中大于0,小于1的数clc; a0=300;b 2020-05-16 …
下列命题中不正确的是A.任意a,b∈R,an=a*n+b,有{an}是等差数列B.存在a,b∈R, 2020-07-30 …
基本不等式的取值范围a、b∈R,a^2+b^2≥2aba、b∈R+,a+b≥2√ab为什么a、b∈ 2020-08-03 …
设三元方程组ax=b,r(a)=2,有3个特解a1,a2,a3,且有a1+a2+a3=(1,1,1 2020-08-03 …
lingo中如何用a,b来代表常数min=(a^2+r^2-2*a*r*cos(c1))^(1/2) 2020-11-06 …
(理科)给出下面四个推导过程:其中正确的推导为①∵a,b∈R+,∴=2;②∵x,y∈R+,∴lgx+ 2020-11-21 …