早教吧作业答案频道 -->数学-->
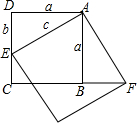
如图,四边形ABCD边长为a的正方形,点E在CD上,DE=b,AE=c,延长CB至点F,使BF=b,连接AF,试利用此图证明勾股定理.
题目详情
如图,四边形ABCD边长为a的正方形,点E在CD上,DE=b,AE=c,延长CB至点F,使BF=b,连接AF,试利用此图证明勾股定理.

▼优质解答
答案和解析
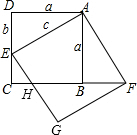
证明:过E作AE的垂线,过F作AF的垂线,两垂线交于点G,设EG与CF交于点H.
在△ADE与△ABF中,
,
∴△ADE≌△ABF(SAS),
∴AE=AF=c,∠DAE=∠BAF,
∴∠EAF=∠EAB+∠BAF=∠EAB+∠DAE=∠DAB=90°,
∵∠AEG=∠AFG=∠EAF=90°,
∴四边形AEGF是矩形,
∵AE=AF=c,
 ∴矩形AEGF是正方形,
∴矩形AEGF是正方形,
∴GF=c,∠G=90°.
在△FGH与△ABF中,
,
∴△FGH∽△ABF,
∴
=
=
,即
=
=
,
∴GH=
,FH=
,
∴CH=BC+BF-FH=a+b-
.
∵S正方形AEGF+S△ADE+S△ECH=S正方形ABCD+S△ABF+S△FGH,S△ADE=S△ABF,
∴S正方形AEGF+S△ECH=S正方形ABCD+S△FGH,
即c2+
(a-b)(a+b-
)=a2+
•
•c,
整理得c2=a2+b2.
在△ADE与△ABF中,
|
∴△ADE≌△ABF(SAS),
∴AE=AF=c,∠DAE=∠BAF,
∴∠EAF=∠EAB+∠BAF=∠EAB+∠DAE=∠DAB=90°,
∵∠AEG=∠AFG=∠EAF=90°,
∴四边形AEGF是矩形,
∵AE=AF=c,
 ∴矩形AEGF是正方形,
∴矩形AEGF是正方形,∴GF=c,∠G=90°.
在△FGH与△ABF中,
|
∴△FGH∽△ABF,
∴
| FG |
| AB |
| GH |
| BF |
| FH |
| AF |
| c |
| a |
| GH |
| b |
| FH |
| c |
∴GH=
| bc |
| a |
| c2 |
| a |
∴CH=BC+BF-FH=a+b-
| c2 |
| a |
∵S正方形AEGF+S△ADE+S△ECH=S正方形ABCD+S△ABF+S△FGH,S△ADE=S△ABF,
∴S正方形AEGF+S△ECH=S正方形ABCD+S△FGH,
即c2+
| 1 |
| 2 |
| c2 |
| a |
| 1 |
| 2 |
| bc |
| a |
整理得c2=a2+b2.
看了 如图,四边形ABCD边长为a...的网友还看了以下:
8、如图888888,已知,A、D、B、C、在同一直线上,AB=CD,AE=DF,BE=CE,那么 2020-04-25 …
在平行四边形ABCD中,点EF分别在BC,AD上,如果点E,F分别是由下列各种情况得到的,那么四边 2020-05-13 …
在长方体ABCD-A1B1C1D1中,E,P分别是BC,A1D1的中点,M,N分别是AE,CD1的 2020-05-16 …
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交A 2020-05-22 …
如图,∠B=∠C,B、A、D在同一条直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,试说明A 2020-06-22 …
如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:△AEF≌△BCD. 2020-06-27 …
图,菱形纸片ABCD中,角A=60°,将纸片折叠,点A,D分别落在A'D'处,且A'D'经过BEF 2020-07-06 …
求含元音字母且发元音的开音和闭音比如:A|ei|就是含有A且发|ei|的音的单词越多越好如:lat 2020-07-14 …
急,在线等已知AB:DB=AC:EC,且AE:EC=3:4,BD-AD=7,求AD长已知AB:DB= 2020-11-21 …
如图,平行四边形ABCD中,AB=2,线段CD的中垂线为AE,垂足为E,将△DAE沿AE翻折到△A' 2020-12-25 …