早教吧作业答案频道 -->数学-->
给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.(1)以下四边形中,是勾股四边形的为.(填写序号即可)①矩形;②有一
题目详情
给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)以下四边形中,是勾股四边形的为___.(填写序号即可)
①矩形;②有一个角为直角的任意凸四边形;③有一个角为60°的菱形.
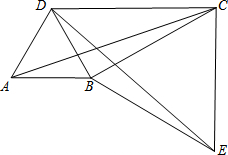
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,∠DCB=30°,连接AD,DC,CE.
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形.

(1)以下四边形中,是勾股四边形的为___.(填写序号即可)
①矩形;②有一个角为直角的任意凸四边形;③有一个角为60°的菱形.
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,∠DCB=30°,连接AD,DC,CE.
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形.
▼优质解答
答案和解析
(1)①如图,
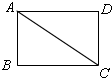
∵四边形ABCD是矩形,
∴∠B=90°,
∴AB2+BC2=AC2,
即:矩形是勾股四边形,
②如图,
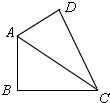
∵∠B=90°,
∴AB2+BC2=AC2,
即:由一个角为直角的四边形是勾股四边形,
③有一个角为60°的菱形,邻边边中没有直角,所以不满足勾股四边形的定义,
故答案为①②,
(2)①∵△ABC绕点B顺时针旋转了60°到△DBE,
∴BC=BE,∠CBE=60°,
∵在△BCE中,BC=BE,∠CBE=60°
∴△BCE是等边三角形.
②∵△BCE是等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=90°,
在Rt△DCE中,有DC2+CE2=DE2,
∵DE=AC,BC=CE,
∴DC2+BC2=AC2,
∴四边形ABCD是勾股四边形.

∵四边形ABCD是矩形,
∴∠B=90°,
∴AB2+BC2=AC2,
即:矩形是勾股四边形,
②如图,

∵∠B=90°,
∴AB2+BC2=AC2,
即:由一个角为直角的四边形是勾股四边形,
③有一个角为60°的菱形,邻边边中没有直角,所以不满足勾股四边形的定义,
故答案为①②,
(2)①∵△ABC绕点B顺时针旋转了60°到△DBE,
∴BC=BE,∠CBE=60°,
∵在△BCE中,BC=BE,∠CBE=60°
∴△BCE是等边三角形.
②∵△BCE是等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=90°,
在Rt△DCE中,有DC2+CE2=DE2,
∵DE=AC,BC=CE,
∴DC2+BC2=AC2,
∴四边形ABCD是勾股四边形.
看了 给出如下定义:若一个四边形中...的网友还看了以下:
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边 2020-05-12 …
(7分)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为 2020-05-12 …
(2007•鄂尔多斯)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则 2020-05-12 …
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边 2020-05-14 …
我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.并发现了“勾股定理”.若直角三 2020-07-10 …
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足,则称这个三角形为勾股三角 2020-07-22 …
定义:若三角形三个内角的度数分别是x、y和z,满足x2+y2=z2,则称这个三角形为勾股三角形.( 2020-07-26 …
给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.( 2020-07-26 …
如图四边形的两条对角线互相垂直,我们把这种四边形叫做勾股四边形勾股四边形ABCD的两条边长a=6, 2020-08-03 …
“实现投资主体多元化,使股份制成为公有制的主要实现形式。”这是因为股份制是A.公有制经济的一种形式B 2020-11-06 …