早教吧作业答案频道 -->数学-->
定义:若三角形三个内角的度数分别是x、y和z,满足x2+y2=z2,则称这个三角形为勾股三角形.(1)根据上述定义,“直角三角形是勾股三角形”是真命题还是假命题;(2)已知一勾股三角
题目详情
定义:若三角形三个内角的度数分别是x、y和z,满足x2+y2=z2,则称这个三角形为勾股三角形.
(1)根据上述定义,“直角三角形是勾股三角形”是真命题还是假命题;
(2)已知一勾股三角形三个内角从小到大依次为x、y和z,且xy=2160,求x+y的值;
(3)如图,△ABC中,AB=
,BC=2,AC=1+
,求证:△ABC是勾股三角形.

(1)根据上述定义,“直角三角形是勾股三角形”是真命题还是假命题;
(2)已知一勾股三角形三个内角从小到大依次为x、y和z,且xy=2160,求x+y的值;
(3)如图,△ABC中,AB=
| 6 |
| 3 |
▼优质解答
答案和解析
(1) “直角三角形是勾股三角形”是假命题;理由如下:
∵对于任意的三角形,设其三个角的度数分别为x°、y°和z°,
若满足x2+y2=z2,则称这个三角形为勾股三角形,
∴无法得到,所有直角三角形是勾股三角形,故是假命题;
(2) 由题意可得:
,
解得:x+y=102;
(3)证明:过B作BH⊥AC于H,如图所示: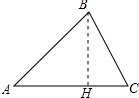
设AH=x
Rt△ABH中,BH=
,
Rt△CBH中,(
)2+(1+
-x)2=4,
解得:x=
,
∴AH=BH=
,HC=1,
∴∠A=∠ABH=45°,
∴tan∠HBC=
=
=
,
∴∠HBC=30°,
∴∠BCH=60°,∠B=75°,
∴452+602=752
∴△ABC是勾股三角形.
∵对于任意的三角形,设其三个角的度数分别为x°、y°和z°,
若满足x2+y2=z2,则称这个三角形为勾股三角形,
∴无法得到,所有直角三角形是勾股三角形,故是假命题;
(2) 由题意可得:
|
解得:x+y=102;
(3)证明:过B作BH⊥AC于H,如图所示:

设AH=x
Rt△ABH中,BH=
| 6-x2 |
Rt△CBH中,(
| 6-x2 |
| 3 |
解得:x=
| 3 |
∴AH=BH=
| 3 |
∴∠A=∠ABH=45°,
∴tan∠HBC=
| HC |
| BH |
| 1 | ||
|
| ||
| 3 |
∴∠HBC=30°,
∴∠BCH=60°,∠B=75°,
∴452+602=752
∴△ABC是勾股三角形.
看了 定义:若三角形三个内角的度数...的网友还看了以下:
三角形与2次函数a、b、c为△ABC的三边,且关于X的一元二次方程(c-b)x^2+(b-a)x+ 2020-04-27 …
已知三角形ABC的一个内角为120度,并且三边长构成公差为4的等差数列,则三角形A BC的面积?: 2020-05-16 …
已知直角三角形三边常为5.12.13,将斜边延长x,较长的直角边延长x+2,x长为多少?已知直角三 2020-05-20 …
如图,0为矩形ABCD的对角线交点,将直角三角形的直角顶点与0点重合,转动三角形使两直角边始终与B 2020-06-06 …
对于一个三角形设其三个内角的度数为X、Y、Z.若x、Y、Z满足X^2+Y^2=Z^2,我们定义这个 2020-06-12 …
一个三角形,角2是角1的2倍,角3的度数是角2的3倍,求角1,角2,角3各是多少度. 2020-06-12 …
2道数学题,哥哥姐姐帮忙,1.圆+圆+圆=三角形+三角形方框+方框=三角形(4个)圆+圆+方框=0 2020-07-30 …
已知三角形ABC两边AB、AC的长是关于X的一元二次方程x^2-(2k+1)x+k(k+1)=0的 2020-08-02 …
三角形角2平分线夹角与顶角的关系具体分类讨论1内角平分线1外角平分线,2外角平分线,2内角平分线( 2020-08-03 …
三角形与2次函数a、b、c为△ABC的三边,且关于X的一元二次方程(c-b)x^2+(b-a)x+ 2020-08-03 …