早教吧作业答案频道 -->数学-->
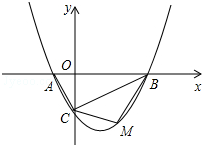
如图,抛物线y=ax2-32x-2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;(3)若
题目详情
如图,抛物线y=ax2-
x-2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
| 3 |
| 2 |

(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
▼优质解答
答案和解析
(1)将B(4,0)代入抛物线的解析式中,得:
0=16a-
×4-2,即:a=
;
∴抛物线的解析式为:y=
x2-
x-2.
(2)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
(3)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=x-2;
设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b=x2-x-2,即:x2-2x-2-b=0,且△=0;
∴4-4×(-2-b)=0,即b=4;
∴直线l:y=x-4.
由于S△MBC=BC×h,当h最大(即点M到直线BC的距离最远)时,△ABC的面积最大
所以点M即直线l和抛物线的唯一交点,有:
,
解得:
,
即M(2,-3).
0=16a-
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
(3)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=x-2;
设直线l∥BC,则该直线的解析式可表示为:y=x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b=x2-x-2,即:x2-2x-2-b=0,且△=0;
∴4-4×(-2-b)=0,即b=4;
∴直线l:y=x-4.
由于S△MBC=BC×h,当h最大(即点M到直线BC的距离最远)时,△ABC的面积最大
所以点M即直线l和抛物线的唯一交点,有:
|
解得:
|
即M(2,-3).
看了 如图,抛物线y=ax2-32...的网友还看了以下:
一道教师招考真题——数学大体如下:f(x)=sinx+(√3)cosx+1求出f(x)对称中心的横 2020-05-23 …
下列变形错误的是.a.若a=b,则a-3=b-3b.若a=b,则7a-1=7b-1c.若a=b,则 2020-06-06 …
直线y=-x-1与抛物线y=ax2+4ax+b交于x轴上A点和另一点D,抛物线交y轴于C点,且CD 2020-06-23 …
已知点A(a,-2)与点B(3,b)关于x轴对称,且点C(a,b)与点D(x,y)关于原点对称,求 2020-07-30 …
摆脱了~(最好有过程)(x+1)^6被x-2除得的余式是多少?多项式x^20+x^7+1除以x^2 2020-07-30 …
已知a,b,c是△ABC的∠A,∠B,∠C对边,a>b,关于x的方程x²-2(a+b)x+2ab+ 2020-07-30 …
A小华看到坐标系中点A关于Y抽的对称点为B[a,b],而点B关于X抽的对称点为C[-3,-2],点 2020-08-01 …
一元一次不等式组x>a-b关于x的不等式组{的解集为1 2020-08-03 …
已知平面直角坐标系中两点A(x,1)、B(-5,y)(1)若点A、B关于x轴对称,则x=,y=;(2 2020-12-25 …
设A等于{X|负一小于等于X大于3}B等于{X|X小于a}若A并B等于B,求a的取值范围 2021-02-04 …