早教吧作业答案频道 -->数学-->
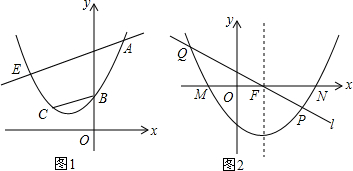
在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2)(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;(2)如图①,若A(1,yA),B(0,yB),C(-1,yC)三点均在C1上,连BC作AE∥BC交
题目详情
在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2)
(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;
(2)如图①,若A(1,yA),B(0,yB),C(-1,yC)三点均在C1上,连BC作AE∥BC交抛物线C1于E,求点E到y轴的距离;
(3)若a=1,将抛物线C1先向右平移3个单位,再向下平移2个单位得到抛物线C2,如图②,抛物线C2与x轴相交于点M、N(M点在N点的左边),抛物线的对称轴交x轴于点F,过点F的直线l与抛物线C2相交于P,Q(P在第四象限)且S△FMQ=2S△FNP,求直线l的解析式.
(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;
(2)如图①,若A(1,yA),B(0,yB),C(-1,yC)三点均在C1上,连BC作AE∥BC交抛物线C1于E,求点E到y轴的距离;
(3)若a=1,将抛物线C1先向右平移3个单位,再向下平移2个单位得到抛物线C2,如图②,抛物线C2与x轴相交于点M、N(M点在N点的左边),抛物线的对称轴交x轴于点F,过点F的直线l与抛物线C2相交于P,Q(P在第四象限)且S△FMQ=2S△FNP,求直线l的解析式.

▼优质解答
答案和解析
(1)根据题意得△=42-4•a•4a=0,解得a1=1,a2=-1,
而0所以a=1,
所以此时C1的解析式为y=x2+4x+4;
(2)根据题意得A(1,5a+4),B(0,4a),C(-1,5a-4),
设直线BC的解析式为y=kx+4a,
把C(-1,5a-4)代入得-k+4a=5a-4,解得k=4-a,
∴直线BC的解析式为y=(4-a)x+4a,
∵BC∥AE,
∴AE的解析式可设为y=(4-a)x+n,
把A(1,5a+4)代入得4-a+n=5a+4,解得n=6a,
∴直线AE的解析式为y=(4-a)x+6a,
方程组
消去y得x2+x-2=0,解得x1=1,x2=-2,
∴E点的横坐标为-2,
∴点E到y轴的距离为2;
(3)作QA⊥x轴于A,PB⊥x轴于B,如图,
当a=1时,y=x2+4x+4=(x+2)2,抛物线C1的顶点坐标为(-2,0),把点(-2,0)先向右平移3个单位,再向下平移2个单位得到对应点的坐标为(1,-2),
所以抛物线C2的解析式为y=(x-1)2-2,即y=x2-2x-1,则抛物线的对称轴为直线x=1,所以F(1,0)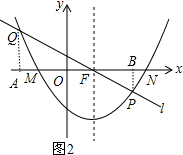
∵抛物线C2与x轴相交于点M、N(M点在N点的左边),
∴FM=FN,
∵S△FMQ=2S△FNP,
∴QA=2PB,
∵AQ∥PB,
∴
=
=2,即FA=2BF,
设P(t,t2-2t-1),则BF=t-1,
∴AF=2(t-1),
∴OA=2(t-1)-1=2t-3,
∴Q[3-2t,(3-2t)2-2(3-2t)-1]
∴(3-2t)2-2(3-2t)-1=-2(t2-2t-1),
整理得t2-2t=0,解得t1=0(舍去),t2=2,
∴P(2,-1),Q(-1,2),
设直线PQ的解析式为y=px+q,
把P(2,-1),Q(-1,2)代入得
,解得
,
∴直线l的解析式为y=-x+1.
而0
所以此时C1的解析式为y=x2+4x+4;
(2)根据题意得A(1,5a+4),B(0,4a),C(-1,5a-4),
设直线BC的解析式为y=kx+4a,
把C(-1,5a-4)代入得-k+4a=5a-4,解得k=4-a,
∴直线BC的解析式为y=(4-a)x+4a,
∵BC∥AE,
∴AE的解析式可设为y=(4-a)x+n,
把A(1,5a+4)代入得4-a+n=5a+4,解得n=6a,
∴直线AE的解析式为y=(4-a)x+6a,
方程组
|
∴E点的横坐标为-2,
∴点E到y轴的距离为2;
(3)作QA⊥x轴于A,PB⊥x轴于B,如图,
当a=1时,y=x2+4x+4=(x+2)2,抛物线C1的顶点坐标为(-2,0),把点(-2,0)先向右平移3个单位,再向下平移2个单位得到对应点的坐标为(1,-2),
所以抛物线C2的解析式为y=(x-1)2-2,即y=x2-2x-1,则抛物线的对称轴为直线x=1,所以F(1,0)

∵抛物线C2与x轴相交于点M、N(M点在N点的左边),
∴FM=FN,
∵S△FMQ=2S△FNP,
∴QA=2PB,
∵AQ∥PB,
∴
| FA |
| FB |
| QA |
| PB |
设P(t,t2-2t-1),则BF=t-1,
∴AF=2(t-1),
∴OA=2(t-1)-1=2t-3,
∴Q[3-2t,(3-2t)2-2(3-2t)-1]
∴(3-2t)2-2(3-2t)-1=-2(t2-2t-1),
整理得t2-2t=0,解得t1=0(舍去),t2=2,
∴P(2,-1),Q(-1,2),
设直线PQ的解析式为y=px+q,
把P(2,-1),Q(-1,2)代入得
|
|
∴直线l的解析式为y=-x+1.
看了 在平面直角坐标系中,抛物线C...的网友还看了以下:
已知函数y=f(x)是定义在R上的奇函数,当x>=0时,f(x)=x+x^21.求x<0时,f(x 2020-05-14 …
已知a=五分之一x+2011 b=负五分之一x-2010 c=五分之一x+2012求代数式a^2+ 2020-05-16 …
高一数学题已知函数f(x)=x/ax+b(a、b为常数,且a≠0)满足f(2)=1,f(x)=x有 2020-05-22 …
已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x)?因为f(x) 2020-06-23 …
高一数学集合1.已知集合A={x|f(x)=x}与集合B{x|f(f(x))=x},其中函数f(x 2020-07-21 …
第一提已知全集U={x丨x≤1或x≥2}A={x丨x<1或x>3}B+={x丨x≤1或x>2}求C 2020-07-30 …
已知a=20分之一x+20,b=20分之一x+19,c=20分之一x+21,求代数式a的平方+b的 2020-07-31 …
初一数学题,急!把多项式(a-5)x^3-x^b+3x-b是二次三项式,那么(b-5)x^a-1- 2020-07-31 …
已知直线y等于二分之一x加b是正弦曲线y等于cosx(0小于等于x小于等于2派)的切线,则b值为 2020-08-02 …
关于交集的一些问题,请务必写出过程,说说为什么,详细一点,我数学差理解不了,多谢已知A={x|y=x 2020-12-26 …