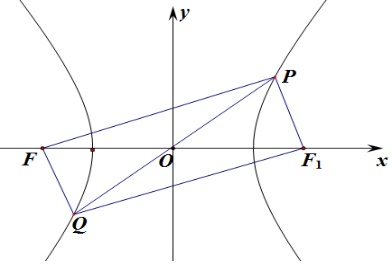
已知双曲线E：x2a2-y2b2=1（a>0，b>0），点F为E的左焦点，点P为E上位于第一象限内的点，P关于原点的对称点为Q，且满足|PF|=3|FQ|，若|OP|=b，则E的离心率为（）A.2B.3C.2D.5

Question

已知双曲线E：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0），点F为E的左焦点，点P为E上位于第一象限内的点，P关于原点的对称点为Q，且满足|PF|=3|FQ|，若|OP|=b，则E的离心率为（　　）

A.

√(2)

B.

√(3)

C. 2

D.

√(5)

Answer 1

由题意可知：双曲线的右焦点F₁，由P关于原点的对称点为Q，
则丨OP丨=丨OQ丨，
∴四边形PFQF₁为平行四边，
则丨PF₁丨=丨FQ丨，丨PF丨=丨QF₁丨，
由|PF|=3|FQ|，根据椭圆的定义丨PF丨-丨PF₁丨=2a，
∴丨PF₁丨=a，|OP|=b，丨OF₁丨=c，
∴∠OPF₁=90°，
在△QPF₁中，丨PQ丨=2b，丨QF₁丨=3a，丨PF₁丨=a，
∴则（2b）²+a²=（3a）²，整理得：b²=2a²，
则双曲线的离心率e=(c)/(a)=√(1+(b2)/(a2))=√(3)，
故选B．